Introductory Olympiad Algebra - This Is Geometry!
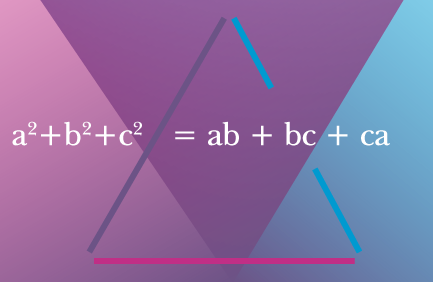 A triangle has side lengths
a
,
b
,
c
which satisfy
A triangle has side lengths
a
,
b
,
c
which satisfy
a 2 + b 2 + c 2 = a b + b c + c a .
Which of the following best describes this triangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
equilateral triangle. Calvin Lin nice solution in brief
is the 0 factor property applied here?
It's not applied here. The property is as such: when we have a finite product of variables equal to 0, at least one of the variables must be equal to 0.
When a real number is squared, it is always non-negative. When the sum non-negative real numbers equals 0, the numbers must all be 0.
The only property that I'm using is called the 'trivial inequality', which states that "squares are non-negative" aka x 2 ≥ 0 .
Can you explain what you mean by "0 factor property"?
very nice >>>it’s good answer
I got it :) great solution calvn lin
Since in Equilateral Triangle all sides and all angles are equal.... it is assumed that a=b=c=k......substitute 'k' in the place of a, b & c in the given equation.... =>>>> k^2+k^2+k^2 = k k+k k+k*k =>>>>> 3k^2=3k^2... since it satisfy the given equation.... Its an equilateral Triangle..
a^2+b^2+c^2=ab+bc+ca,if and only if ab=a^2 and bc=b^2 or ca=c^2 which means a=b=c(triangle is equilateral)
How did you conclude that a 2 + b 2 + c 2 = a b + b c + c a if and only if a b = a 2 , b c = b 2 , c a = c 2 ? Are you trying to say that if A + B + C = D + E + F then we must have A = D , B = E , C = F ?
By the Cauchy-Schwarz inequality,
( a 2 + b 2 + c 2 ) ( b 2 + c 2 + a 2 ) ≥ ( a b + b c + c a ) 2 ( a 2 + b 2 + c 2 ) 2 ≥ ( a b + b c + c a ) 2 .
Thus, we have
a 2 + b 2 + c 2 ≥ a b + b c + c a .
Therefore, equality must hold. Equality holds in the Cauchy-Schwarz inequality if and only if the two sequences on the left-hand side are proportional:
b a = c b = a c . However, b a ⋅ c b ⋅ a c = 1 , so we must have
b a = c b = a c = 1 ,
so a = b = c and thus the triangle is equilateral. □
need not to be so complex!
this is super elegant
We can solve this question by factorising the given expression.
a 2 + b 2 + c 2 = a b + b c + c a
a 2 + b 2 + c 2 − ( a b + b c + c a ) = 0
a 2 + b 2 + c 2 − a b − b c − c a = 0
2 × ( a 2 + b 2 + c 2 − a b − b c − c a ) = 2 × 0
2 a 2 + 2 b 2 + 2 c 2 − 2 a b − 2 b c − 2 c a = 0
a 2 + a 2 + b 2 + b 2 + c 2 + c 2 − 2 a b − 2 b c − 2 c a = 0
a 2 − 2 a b + b 2 + b 2 − 2 b c + c 2 + c 2 − 2 c a + a 2 = 0
( a − b ) 2 + ( b − c ) 2 + ( c − a ) 2 = 0
So, ( a − b ) 2 = 0 , ( b − c ) 2 = 0 and ( c − a ) 2 = 0
So, a − b = 0 , b − c = 0 and c − a = 0
So, a = b , b = c and c = a
This suggests that: a = b = c (All sides are equal)
So, the answer is an E q u i l a t e r a l triangle.
If we assume that abc is an equilateral triangle, then the triangle will be equilateral. Your argument is circular.
I have posted a more appropriate solution to this question.
Clearly he starts by assuming what is to be shown and that is wrong but if you see that the given question is a multiple choice single correct answer question so if u assume any of the options as correct and dont get a contradiction then that option should be correct right?
Not necessarily so, even with your logic. This is because you are asked to find the best option. For example, it could be true for "isosceles triangles" or "acute triangles" or "all triangles", which would have been better descriptions.
The given expression is equivalent to (a - b)^2 + (b - c)^2 + (c - a)^2 = 0 Since squares are non-negative, the only way that their sum can be equal to 0, is for all of them to be 0. Hence, we have a - b = 0 , b - c = 0 ,c - a = 0, or that a = b = c . Thus, we have an equilateral triangle.
By AM-GM A^2 + B^2 ≥ to 2AB. B^2 + C^2 ≥ 2BC . A^2 + C^2 ≥ 2AC. Adding all a^2 + b^2 +c^2 is ≥ ab + bc + ca. equality holds when a=b=c.Hence triangle is equilateral (note sides are positive hence we can apply AM -GM)
Using the law of cosine a2=b2+c2-2bccosA, b2=c2+a2-2cacosB, c2=a2+b2-2abcosC Adding all the 3 and simplifying gets a2+b2+c2-2(abcosC+bccosA+cacosB)=0 Replacing a2+b2+c2 with ab+bc+ca results in bc(1-2cosA)+ca(1-2cosB)+ab(1-2cosC)=0 Therefore cosA, cosB, cosC =1/2 So angle A, B and C are 60 degree Hence an equilateral triangle
The given expression is equivalent to
( a − b ) 2 + ( b − c ) 2 + ( c − a ) 2 = 0
Since squares are non-negative, the only way that their sum can be equal to 0, is for all of them to be 0. Hence, we have a − b = 0 , b − c = 0 , c − a = 0 , or that a = b = c . Thus, we have an equilateral triangle.