Inverse trigonometry-JEE

Let $\sin^{-1}x$ $= \alpha$ $\Rightarrow$ $\sin\alpha = x$

And, let $\sin^{-1}2x$ $= \beta$ $\Rightarrow$ $\sin\beta = 2x$

Then, we have, $\alpha + \beta = \frac{\pi}{3}$ and $\sin\alpha = x$ and $\sin\beta = 2x$ .

So, $\cos\alpha = \sqrt{1 - \sin^2 \alpha}$ $= \sqrt{1 - x^2}$

And, $\cos\beta = \sqrt{1 - \sin^2 \beta}$ $= \sqrt{1 - 4x^2}$

So, now, $\cos(\alpha+\beta) = \cos\frac{\pi}{3}$

$\Rightarrow$ $\cos\alpha\cos\beta - \sin\alpha\sin\beta = \frac{1}{2}$

$\Rightarrow$ $\sqrt{(1-x^2)(1-4x^2)} - 2x^2 = \frac{1}{2}$

$\Rightarrow$ $\sqrt{(1-x^2)(1-4x^2)} = \frac{4x^2+1}{2}$

$\Rightarrow$ $1 - 5x^2 + 4x^4 = \frac{16x^4 + 8x^2 + 1}{4}$

$\Rightarrow$ $4 - 20x^2 + 16x^4 = 16x^4 + 8x^2 + 1$

$\Rightarrow$ $x^2 = \frac{3}{28}$

$\Rightarrow$ $x = \sqrt{\frac{3}{28}} = 0.327 (approx.)$

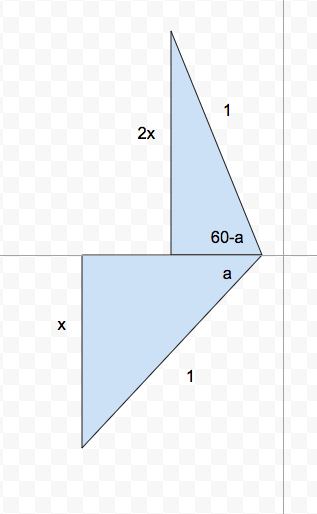
We can consider two Right Triangles as shown in the diagram, both with a hypotenuse of $1$ and both share a side on the same line. The opposite side of one Triangle is $x$ and the opposite side of the other Triangle is $2x$ . Since $arcsin(x)+arcsin(2x) = 60°$ , the angle between the hypotenuses is $60°$ . If the angle opposite to $x$ is $a$ and the angle opposite to $2x$ is $60-a$ , $2sin(a)=sin(60-a)$ . Expanding $sin(60-a)$ and using the pythagorean identity to substitute $cos(a)$ with the square root of $1-sin(a)^2$ , we get $sin(a) = 0.327 = x$ , which is the final answer.