Inversing the cotangent
1 0 cot [ cot − 1 ( 3 ) + cot − 1 ( 7 ) + cot − 1 ( 1 3 ) + cot − 1 ( 2 1 ) ] = ?
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
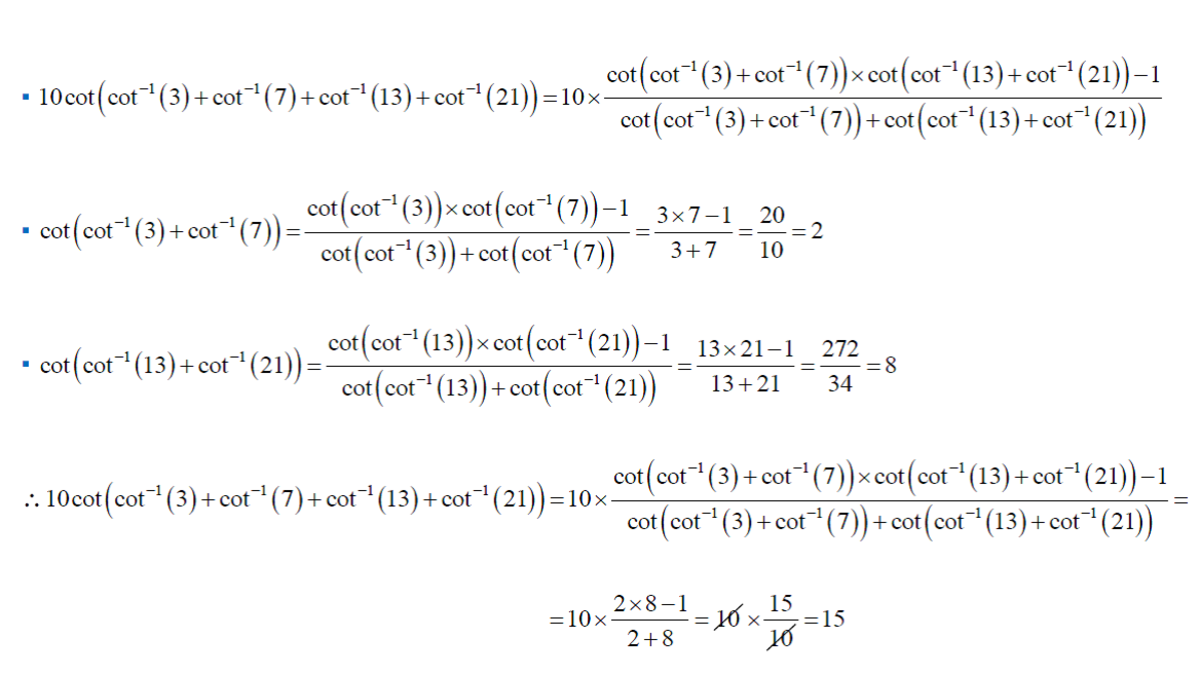
Moderator note:
Right. For the sake of variety, can you think of another approach?
First, consider the following. For complex numbers z 1 , z 2 , … , z n :
a r g ( z 1 z 2 … z n ) = a r g ( z 1 ) + a r g ( z 2 ) + ⋯ + a r g ( z n )
Where z = a + b i , a r g ( z ) = c o t − 1 ( b a )
Therefore we have the following formula:
cot ( k = 1 ∑ n c o t − 1 ( z k ) ) = I m [ p ] R e [ p ] where p = z 1 z 2 … z n
In this case, p = ( 3 + i ) ( 7 + i ) ( 1 3 + i ) ( 2 1 + i ) = 5 1 0 0 + 3 4 0 0 i
R e [ p ] = 5 1 0 0 , I m [ p ] = 3 4 0 0 , and I m [ p ] R e [ p ] = 2 3 .
Plugging this into our problem, our answer becomes 1 0 ( 2 3 ) = 1 5
cot^(-1)(x)+cot^(-1)(y)=cot^(-1)[(xy-1)/x+y] Using the above formula we get cot^(-1)(3)+cot^(-1)(7)=cot^(-1)(2) and cot^(-1)(13)+cot^(-1)(21)=cot^(-1)(8) Again cot^(-1)(2)+cot^(-1)(8)=cot^(-1)(3/2). Now 10cot[cot^(-1)(3/2)]=10*3/2=15(Answer)
Stop being unoriginal and copying AIME problems! Seriously, its really annoying!
1 0 c o t [ c o t − 1 ( 3 ) + c o t − 1 ( 7 ) + c o t − 1 ( 1 3 ) + c o t − 1 ( 2 1 ) ] 1 0 c o t [ t a n − 1 3 1 + t a n − 1 7 1 + t a n − 1 1 3 1 + t a n − 1 2 1 1 ] 1 0 c o t [ t a n − 1 2 1 + t a n − 1 8 1 ] 1 0 c o t [ t a n − 1 1 5 1 0 ] = 1 0 c o t [ c o t − 1 1 0 1 5 ] 1 5
Formulas used above :
t a n − 1 x + t a n − 1 y = t a n − 1 1 − x y x + y
c o t − 1 x = t a n − 1 x 1 and vice-versa