Iotic iota?
What is
i 2 + i 6 + i 4 ?
Note: i is the imaginary number − 1 .
The answer is -1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
29 solutions
wth I wrote -1 and it said my answer was incorrect. Then it revealed the answer was -1. I the had correct answer
Now I understand.
it is easy question , please send more like this
That's a nice way to solve any question.... Thankx Bilal.. :)
Thanks bilal for such nice explanation..
I tried to write the answer but my cellphone keyboard didn't have the minus... I knew the answer 😪
with calculation it is -1, if you see conceptully if you rotate 1 for 12 times, i.e 2+4+6, it is 1 again. and i have one more doubt.. if the expression is i2+i6+i6, is the value is -3? or -1?... is it possible to get lower or higher than -1 with only using i....please think and help to understand i better...because it is imaginary number... and took lot of time for me to understand i conceptually..
Log in to reply
Yes, i^2 + i^6 + i^6 would equal -3 because each of those equals -1.
If i = sqrt(-1), then it follows that i^2 = -1. This is because (sqrt(x))^2 = x, replace x with -1 and it still holds true.
Our expression is i^2 + i^6 + i^4, which can be changed into a form more easily understood: i^2 + (i^2)^3 + (i^2)^2. Now if i^2 = -1, then this becomes (-1) + (-1)^3 + (-1)^2. (-1)^3 = -1, and (-1)^2 = 1. So our expression becomes (-1) + (-1) + 1 = -1
I m also having problem I didn't find 'minus'sign my phone keypad while answering the question.
i^2 + i^6 + i^4 = i = √-1
Log in to reply
i = − 1
@Viswa Prasad i =√-1 So i^2 = (√-1)^2 = -1
i = − 1
So i 2 = − 1 .
⇒ i 6 = ( i 2 ) 3 = − 1
And i 4 = 1 .
So the ans is -1. □
How I=-1 . Its not given in the Question
Log in to reply
In mathematics "i" is an imaginary number i=root (-1). Since you can not take the square root of a negative number it's imaginary. Yes the fact that i is root -1 is not given, but it's prior knowledge for most.
You just gotta know that part
i=sqrt(-1) , thats defined
Thanks for your confirmation i=sqrt(-1)
If we take i^6= (i^3)^2=1.....the answer is coming as 1...what's wrong here
Log in to reply
(i^3)^2=(-i)^2=+i^2=i^2= -1 Hope this helps!
Why in the root there is a negative numeral?
your solution is so messy and untidy
I don't understand your explanation it's just so simple can you show off a little bit of challenge to your explanation
Since i = − 1 , then i 2 = − 1 ,
then i 6 = ( i 2 ) 3 = ( − 1 ) 3 = − 1
and i 4 = ( i 2 ) 2 = ( − 1 ) 2 = 1 .
Therefore:
i 2 + i 6 + i 4 = − 1 + ( − 1 ) + ( 1 ) = − 2 + 1 = − 1
i^2 = -1 therefore: i^2 + (i^2)(i^2)(i^2) + (i^2)(i^2) = -1+(-1)(-1)(-1) +(-1)(-1) = -1 ans...
(-1)^2+(-1)^6+(-1)^=-1+(-1)+1=-1
i is an sqrt of -1. i^2 is -1, i^6 is {sqrt(-1)}^6 so (-1)^3. It is -1, i^4 is {sqrt(-1)}^4 So (-1)^2. It is 1. In total, -1-1+1 is -1.
i^2 + i^6 + i^4 = (i^^2) (1 + i^4 + i^2) = (-1) (1 + 1 + (-1)) = (-1)*(1) = -1
Same solution as @Bilal Khan
i 2 + i 6 + i 4 = i 2 + ( i 2 ) 3 + ( i 2 ) 2 = − 1 + ( − 1 ) 3 + ( − 1 ) 2 = − 1 + − 1 + 1 = − 1
As we know, i^2=-1. i^3 can be written as i(-1)=-i i^4 is (-i)i=1 i^5 is 1(i) = i i^6 is i(i) which is also i^2=-1
So (i^2)+(i^6)+(i^4) is -1 + -1 + 1 = -1
i^{2} + i^{6} + i^{4}
i^{2} = (√-1)^{2} = -1
i^{6} = (√-1)^{6} = (-1)^{3} = -1
i^{4} = (√-1)^{4} = (-1)^{2} = 1
-1-1+1 = -1
(i^2= -1+ i^6= -1+ i^4= 1)= -1
i^2+i^6+i^4 = i^2(1+i^4+i^2) = -1(1+i^4-1) = -(i^2)^2 = -(-1)^2 = -1*1 = -1
as i=-1^1/2 i2=-1 i6 =-1 i4=1 so the sum is -1
i^{2} = (-1) hence i^{6} = (-1)^{3} = -1 i^{4} = (-1)^{2} = +1 there fore (-1) + (-1) + (+1) = (-1)
i^2=-1, i^6=-1, i^4=1 ----> (-1)+(-1)+1=-1
= i^2 ( 1 + i^4 + i^2 )
= i^2 { 1 + (i^2)^2 + i^2 }
= i^2 { 1 + (-1)^2 + (-1) } ; [ i^2 = -1]
= i^2 ( 1+ 1 - 1 )
= i^2
= -1 Ans.
i = root -1 i^2 = -1 i^3 = -root - 1 i^4 = 1 This is an ongoing cycle so i^5 goes back to the same value as (i) since it is i^4 x i = 1 x i = i. also, i^6 = i^2, i^7 = i^3, i^8 = i^4 i^9 = i and this is a cycle that goes on forever so this equation will simplify to: -1 -1 + 1 = -1
As i² = -1 , i^4 = (i^2)^2 = (-1)^2 = 1 , i^6 = (i^2)^3 = (-1)^3 = -1
Therefore , -1+(-1) + 1 = -1
since i^2 = -1
therefore i^2 = -1 and i^6 = -1 and i^4 = 1
therefore i^2 + i^6 + i^4 = -1-1+ = -1
ι^2 = -1
ι^2+ι^4+ι^6=(−1)+(−1)^3+(−1)^2
= -1 -1 +1
=-1
why should i ^ 2 be = -1,....cud u help me ??
Log in to reply
its given that 'i' is the square root of -1 hence i^2=-1
i=root(-1) so this way value is -1
But why i = root 1 And then why its square become negative and not positive. .. Please tell me elongative and simpler...clear my concepts...
Log in to reply
It's i = − 1
This is called imaginary number: See here , this too
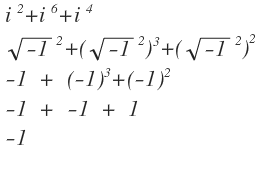
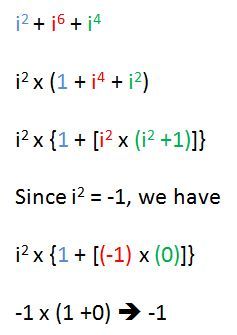
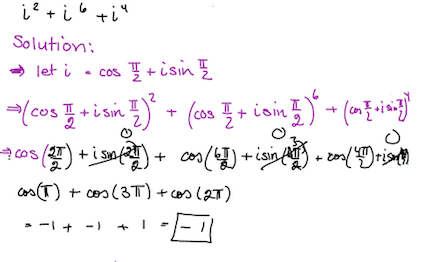
We can write the given expression as i 2 + ( i 2 ) 3 + ( i 2 ) 2 . Since i 2 = − 1 , we substitute it in the above expression. Therefore ( − 1 ) + ( − 1 ) 3 + ( − 1 ) 2 = − 1 + ( − 1 ) + 1 = − 1 . □