IPhO 2014 Theoretical Problem #1
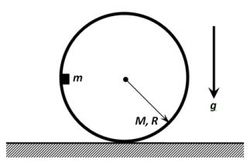 A small puck of mass
m
is carefully placed onto the inner surface of the thin hollow thin cylinder of mass
M
and of radius
R
. Initially, the cylinder rests on the horizontal plane and the puck is located at the height
R
above the plane as shown in the figure on the left. Find the interaction force
F
between the puck and the cylinder at the moment when the puck passes the lowest point of its trajectory. Assume that the friction between the puck and the inner surface of the cylinder is absent, and the cylinder moves on the plane without slipping. The free fall acceleration is
g
.
A small puck of mass
m
is carefully placed onto the inner surface of the thin hollow thin cylinder of mass
M
and of radius
R
. Initially, the cylinder rests on the horizontal plane and the puck is located at the height
R
above the plane as shown in the figure on the left. Find the interaction force
F
between the puck and the cylinder at the moment when the puck passes the lowest point of its trajectory. Assume that the friction between the puck and the inner surface of the cylinder is absent, and the cylinder moves on the plane without slipping. The free fall acceleration is
g
.
F = p m g ( q + M m ) , where p , q are integers. Find p + q .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
I have an idea,if you kindly see if its correct or not,that is-------Let us apply conservation of energy in two different frames. Frame 1:Cylinder CM Frame Frame 2:Ground Frame then you can find the corresponding motion equations
Log in to reply
Is this how you did it? Care to write up your solution?
did you mean m v ˙ x = F N ( t ) c o s θ ( t ) instead of v ˙ x = F N ( t ) c o s θ ( t ) ?
Hello there I have an very easy objective approach to the question,😉😉 Given, F(n)=pmg(q+m/Mp) Consider the case when M>>m , As the cylinder is very heavy it does not move at all hence Energy conservation mgr=1/2m(ωr)^2 ---1 And newton laws for the lowest position F(n)-mg=mω^2r -----2 Solving 1 and 2 gives F(n)=3mg and according to the ques when M>>m F(n)=p.q.mg Hence p.q=3 hence only integer solutions to this satisfies p+q=4
Here i just want to share my idea, not entire solution, which is not contained in the main solution and which can make your calculating a little easier. You know that static friction does not do any work it just convert one energies into another similliar it does not change entire momentum just converting translational into angular and backwards. So in this case you can write that p m R + p M R + L M = 0 like a vectors.
− − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
Consider the forces acting on the puck and the cylinder and depicted in the figure on the right. The puck is subject to the gravity force 𝑚𝑔 and the reaction force from the cylinder 𝑁. The cylinder is subject to the gravity force 𝑀𝑔, the reaction force from the plane 𝑁1 , the friction force 𝐹𝑓𝑟 and the pressure force from the puck 𝑁 ′ = −𝑁. The idea is to write the horizontal projections of the equations of motion. It is written for the puck as follows 𝑚𝑎𝑥 = 𝑁 sin 𝛼, (A.1) where 𝑎𝑥 is the horizontal projection of the puck acceleration. For the cylinder the equation of motion with the acceleration 𝑤 is found as 𝑀𝑤 = 𝑁 sin 𝛼 − 𝐹𝑓𝑟 . (A.2) Since the cylinder moves along the plane without sliding its angular acceleration is obtained as 𝜀 = 𝑤/𝑅 (A.3) Then the equation of rotational motion around the center of mass of the cylinder takes the form 𝐼𝜀 = 𝐹𝑓𝑟𝑅, (A.4) where the inertia moment of the hollow cylinder is given by 𝐼 = 𝑀𝑅 2 . (A.5) Solving (A.2)-(A.5) yields 2𝑀𝑤 = 𝑁 sin 𝛼. (A.6) From equations (A.1) and (A.6) it is easily concluded that 𝑚𝑎𝑥 = 2𝑀𝑤. (A.7) Since the initial velocities of the puck and of the cylinder are both equal to zero, then, it follows from (A.7) after integrating that 𝑚𝑢 = 2𝑀𝑣. (A.8) It is obvious that the conservation law for the system is written as 𝑚𝑔𝑅 = 𝑚𝑢 2 2 + 𝑀𝑣 2 2 + 𝐼𝜔 2 2 , (A.9) where the angular velocity of the cylinder is found to be 𝜔 = 𝑣 𝑅 , (A.10) since it does not slide over the plane. Solving (A.8)-(A.10) results in velocities at the lowest point of the puck trajectory written as 𝑢 = 2 𝑀𝑔𝑅 (2𝑀+𝑚) , (A.12) 𝑣 = 𝑚 𝑀
𝑀𝑔𝑅 (2𝑀+𝑚) . (A.13) In the reference frame sliding progressively along with the cylinder axis, the puck moves in a circle of radius 𝑅 and, at the lowest point of its trajectory, have the velocity 𝑣𝑟𝑒𝑙 = 𝑢 + 𝑣 (A.14) and the acceleration 𝑎rel = 𝑣rel 2 𝑅 . (A.15) At the lowest point of the puck trajectory the acceleration of the cylinder axis is equal to zero, therefore, the puck acceleration in the laboratory reference frame is also given by (A.15). 𝐹 − 𝑚𝑔 = 𝑚𝑣𝑟𝑒𝑙 2 𝑅 . (A.16) then the interaction force between the puck and the cylinder is finally found as 𝐹 = 3𝑚𝑔 1 + 𝑚 3𝑀 . (A.17) *bold text * **
a c c o r d i n g t o l a g r a n g e e q u a t i o n L = 2 1 m v 2 + 2 1 M v 2 + 2 1 I ω 2 thus d v d L = P so the momentum for the cylinder P = 2 M V then putting this in the Lagrange we conclude F=3mg(1-\frac{m}{3M}))
First, we can write the kinetic energy of the system
K.E. = 2 1 m v 2 puck + 2 1 M V 2 + 2 1 M R 2 cylinder ω 2 = 2 1 m v 2 + M V 2
At any given time, this must be equal to the potential energy lost by the puck
P.E. = m g R ( 1 − cos θ )
where θ is the angle between the horizontal, and a radius drawn to the puck (from the center of the cylinder). We'll evaluate this when θ = 0 (puck is at the bottom of its trajectory) and apply it to exploit the conservation of energy. The tricky part of the problem is in finding another conserved quantity, or a work energy-energy relationship to employ.
When the puck falls, it will slide to the right along the surface of the cylinder. At the same time, the cylinder will roll to the left. Relative to the center of mass of the cylinder, both the puck and cylinder have counter-clockwise angular momentum pointing out of the page. This recalls the relationship between angular momentum and torque
Δ L = ∫ τ d t
However, the center of mass isn't the simplest frame to choose because of the applied friction from the floor (rolling without slipping). Instead, let's calculate in the accelerate frame of the cylinder's point of contact with the floor.
In this frame, friction has zero moment arm and doesn't make a contribution. The only torque on the cylinder is from the normal force from the puck to the surface of the cylinder. This has magnitude F N and points along the radius. The perpendicular distance from the puck to the point of contact is given by R cos θ . The moment of inertia of the cylinder about the point of contact is given by the parallel-axis theorem I ′ = I + M R 2 = 2 M R 2 . Thus we have
Δ L 2 M R 2 Ω = ∫ τ d t = ∫ F N ( t ) R cos θ ( t ) d t
which shows 2 M R Ω = ∫ F N ( t ) cos θ ( t ) .
Now notice, in the rest frame of the floor, the acceleration of the puck along the floor is given simply by v ˙ x = F N ( t ) cos θ ( t ) , so that the integral above is just equal to the change in momentum of the puck as it falls to the low point of the trajectory, i.e. ∫ F N ( t ) cos θ ( t ) d t = m v and m v = 2 M R Ω .
We return now to the rest frame of the floor. Since the cylinder rolls without slipping, Ω R = V , and so m v = 2 M V . Inserting this in the energy conservation relation
m g R = 2 1 m v 2 + M ( 2 M m v ) 2 = 2 1 m v 2 ( 1 + 2 M m )
Solving for v , we have
v = 1 + 2 M m 2 g R = 2 M + m 4 g R M = 2 2 M + m g R M
and obviously, V = M m 2 M + m g R M .
Now, the force between the puck and the cylinder has to support the gravitational pull on the puck, plus the centripetal acceleration of the puck in the rest frame of the floor, i.e.
F N = m g + m R ( v + V ) 2 = m g + m ( 2 + M m ) 2 2 M + m g M = m g + M m g ( 2 M + m ) = 3 m g + M m 2 g
or, in the form indicated in the solution
F N = 3 m g ( 1 + 3 M m )