Peculiar Cube

Geometry Level 4

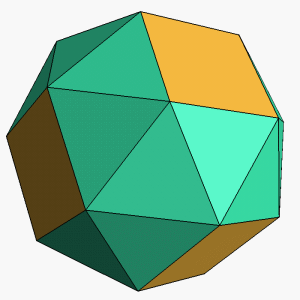
A convex, vertex-transitive polyhedron is composed of squares and equilateral triangles with 5 faces joining at each vertex.

If $x$ is the number of square faces and $y$ is the number of triangle faces, compute $xy.$

The answer is 192.

1 solution

Worranat Pakornrat
Oct 31, 2016

If the solid is convex and regular, then we can apply Euler's characteristics for number of vertices $V$ , edges $E$ , & faces $F$ :

$V - E + F = 2$

Let $x$ = number of squares and $y$ = number of triangles.

Now when constructing this solid, each edge is adhesion between two faces, so $E = \dfrac{4x+3y}{2}$ .

Similarly, when constructing this solid, each vertex is joining of $5$ faces, so $V = \dfrac{4x+3y}{5}$ .

Finally, $F = x + y$ .

Therefore, $\dfrac{4x+3y}{5} - \dfrac{4x+3y}{2} + (x+y) = 2$ .

$(\dfrac{-3}{10})(4x+3y) + x+y = 2$

$\dfrac{-6x}{5} - \dfrac{9y}{10} + x + y = 2$

$\dfrac{y}{10} - \dfrac{x}{5} = 2$

$y - 2x = 20$

Now if we disregard the triangular faces, we can see that the square faces occupy the whole vertices of the solid themselves. That is, $V = 4x$ .

Hence, $4x = \dfrac{4x+3y}{5}$ .

$20x = 4x + 3y$

$16x = 3y$

Plugging in $y = 20 + 2x$ from the first equation:

$16x = 60 + 6x$

Therefore, $x = 6$ , and $y = 32$ .

As a result, $xy = \boxed{192}$ .

I think this is called snub-cube.A very good solution...+1

Ayush G Rai - 4 years, 7 months ago

Right on. That's the term.

Worranat Pakornrat - 4 years, 7 months ago

Another way to solve this problem is by counting the faces in the very good and accurate drawing of the polyhedron.

Michael Mendrin - 4 years, 7 months ago

Now if we disregard the triangular faces, we can see that the square faces occupy the whole vertices of the solid themselves.

It might worth mentioning that you can conclude this because you know a) the polyhedron has at least one square face (there is a polyhedron satisfying the conditions but having no square face, the icosahedron), b) each vertex is incident to at most one square face (if there are two, the sum of angles meeting there is $360^\circ$ ), and c) the polyhedron is vertex-transitive (so each vertex has the exact same configuration of incident faces, thus each vertex is incident to exactly one square face).

Ivan Koswara - 4 years, 7 months ago

Peculiar Cube

The answer is 192.

1 solution

0 pending reports