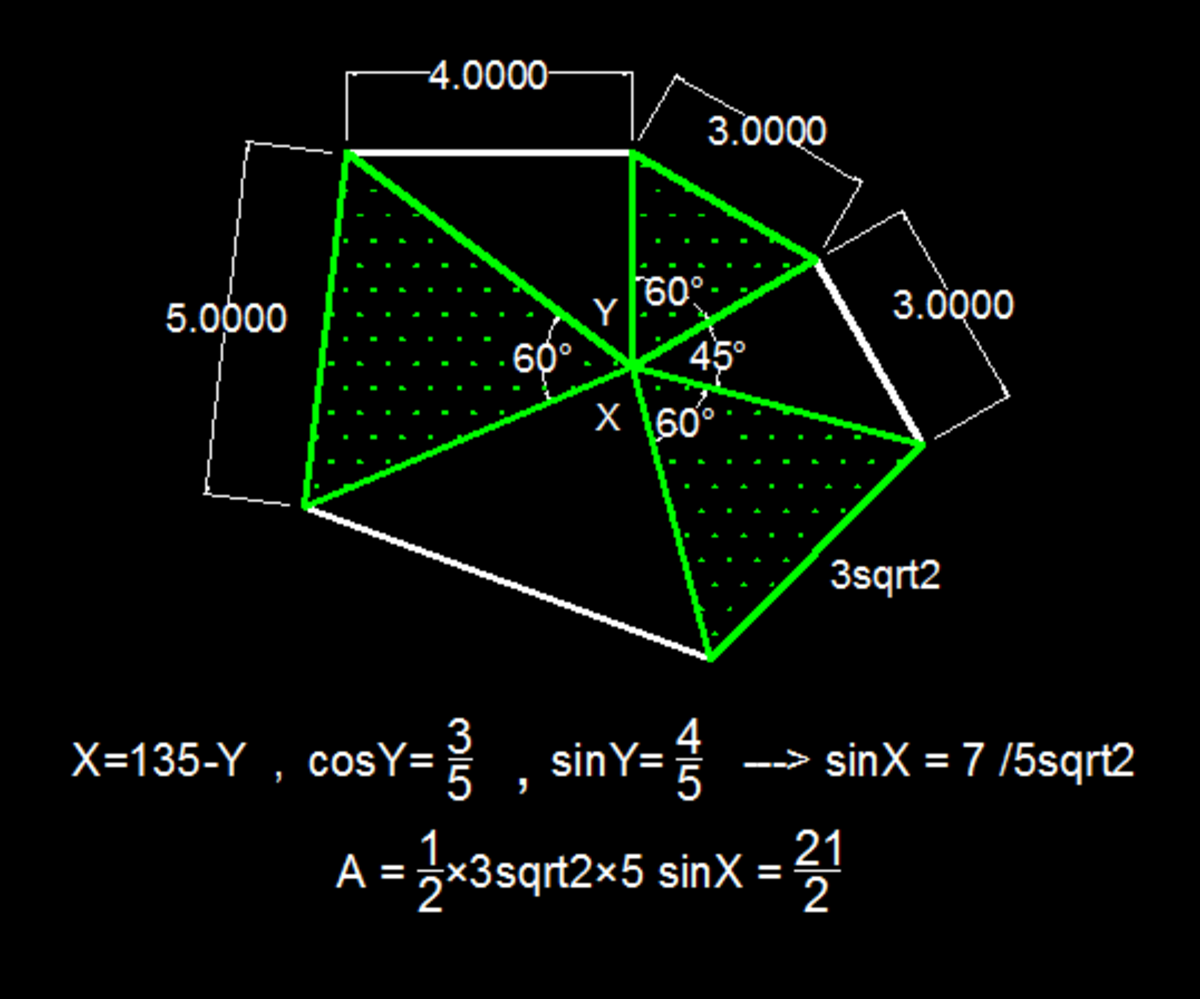
Irregular exagon
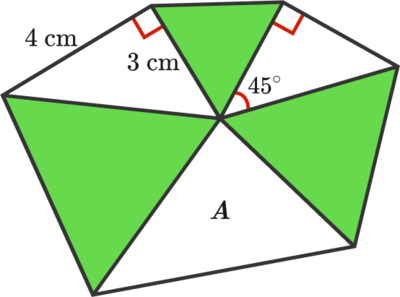
All the green triangles above are equilateral triangles.
What is the area of the triangle labelled as A ( in cm 2 ) ?
The answer is 10.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
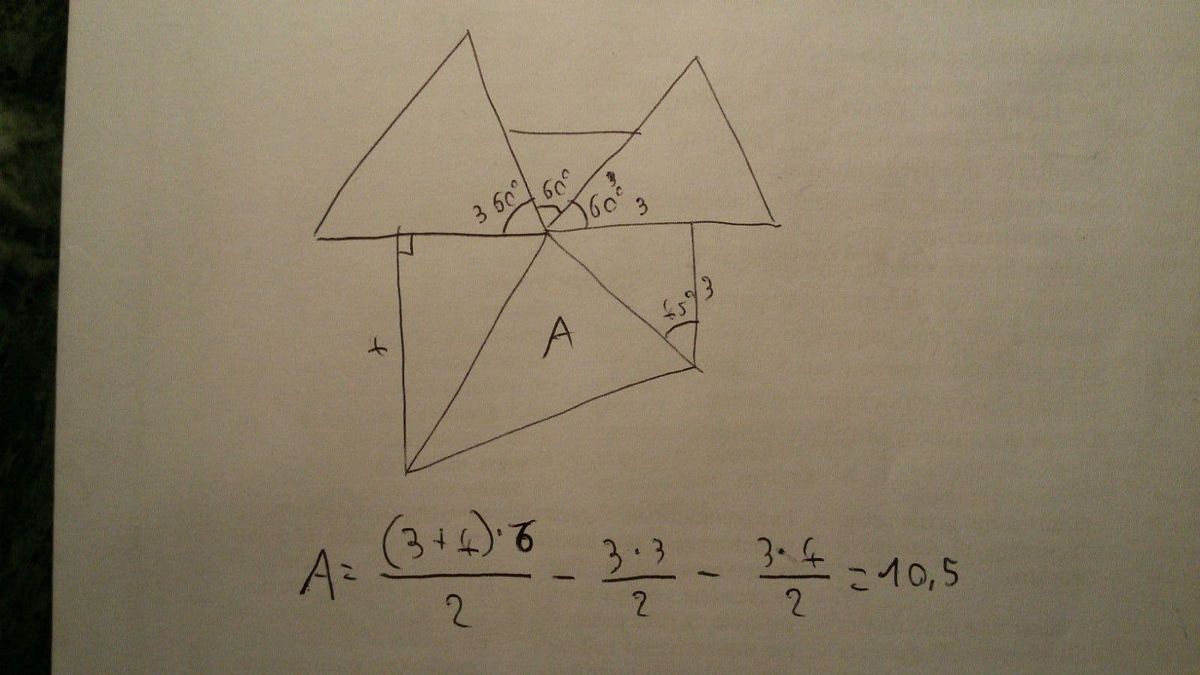 By changing the position of the triangles you get to something like the photo above. Then the area labeled as A is just the area of a rectangular trapezium less the area of white triangles.
By changing the position of the triangles you get to something like the photo above. Then the area labeled as A is just the area of a rectangular trapezium less the area of white triangles.
I've solved it by trigonometry, haven't thought that geometric proof is much simple and easy
The white triangle on the left has a hypotenuse equal 5. So the left side of bottom white triangle is also 5 (since the left green triangle is equilateral). White triangle on the right has left leg equal 3 (since the top green triangle is equilateral), and the right leg also (the 4 5 ∘ -angle makes it an isosceles triangle). So the hypotenuse of the right white triangle, and therefore also the right side of the bottom white triangle, is 3 × 2 . The angle between these two known sides of the bottom white triangle is 3 6 0 ∘ − 3 × 6 0 ∘ − 4 5 ∘ − a r c t a n ( 3 4 ) ≈ 8 1 . 8 7 ∘ . The area A , calculated from two sides and an angle in between, is A = 2 1 × 5 × 3 2 × s i n ( 8 1 . 8 7 ∘ ) = 1 0 . 5
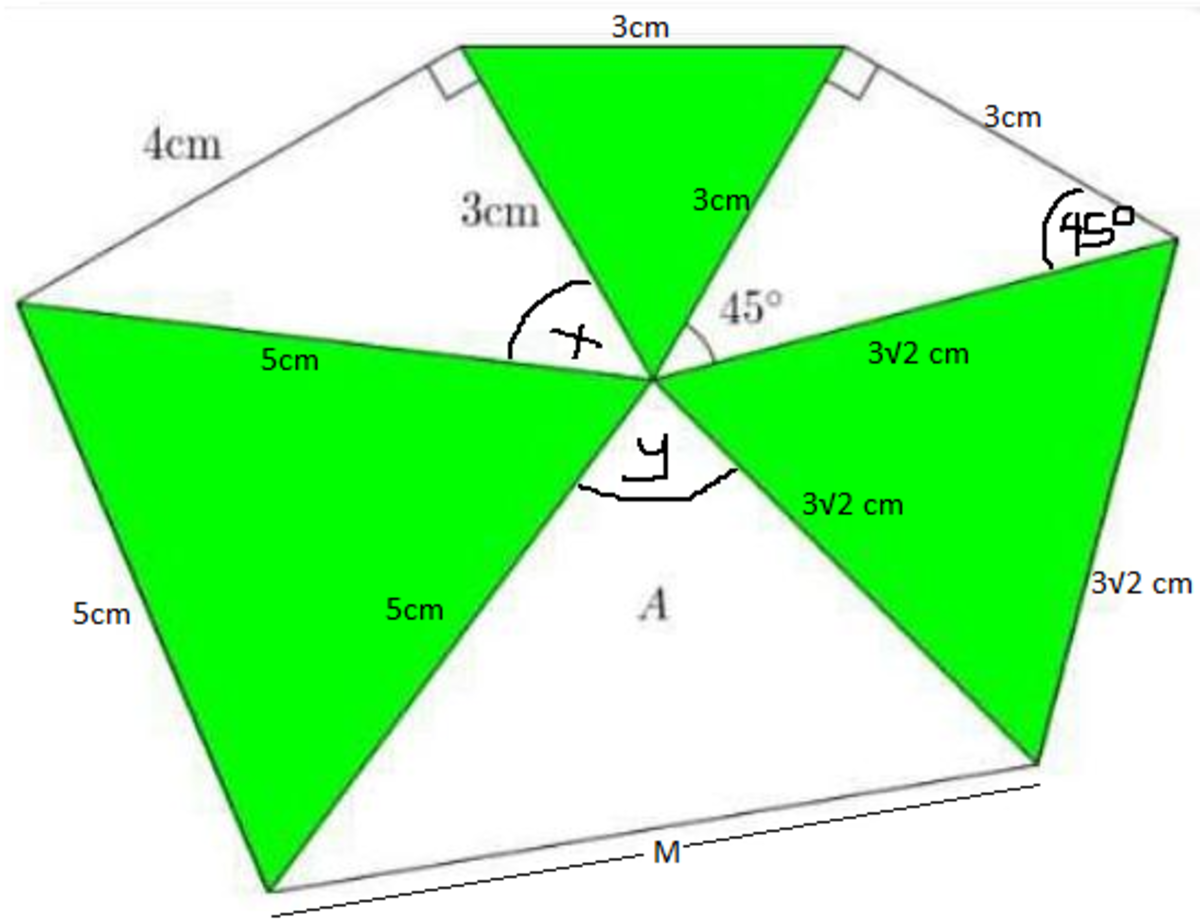
x + y + 4 5 + 6 0 + 6 0 + 6 0 = 3 6 0
y = 1 3 5 − x
Law of Cosine in Triangle A.
M 2 = ( 5 ) 2 + ( 3 2 ) 2 − 2 ( 5 ) ( 3 2 ) cos ( y )
M 2 = 2 5 + 1 8 − ( 3 0 2 ) cos ( 1 3 5 − x )
⇒ cos ( 1 3 5 − x ) = cos ( 1 3 5 ) cos ( x ) + sin ( 1 3 5 ) sin ( x )
⇒ cos ( 1 3 5 − x ) = 2 − 2 ( 5 3 ) + 2 2 ( 5 4 )
⇒ cos ( 1 3 5 − x ) = 1 0 2
M 2 = 2 5 + 1 8 − ( 3 0 2 ) ( 1 0 2 )
M 2 = 4 3 − 6
M = 3 7 cm
Sides of Triangle A: 5 cm , 3 2 cm , and 3 7 cm
Heron's Formula for area of triangle given three sides:
A = p ( p − a ) ( p − b ) ( p − c )
where p = 2 a + b + c
Solving for the area, we get A = 1 0 . 5 cm
Sad to say, that is the way I figured it out, Law of Cosines to get the missing side, the Heron to get the area from sides alone. Seems like it must be the "hard way" but the necessary quantities are easily derived from the given information.