Irregular pyramid
 Sides of a triangular pyramid are right-angled triangles with right angle vertices at the pyramid vertex. Areas of these sides are
,
and
. Volume of the pyramid (in
) is:
Sides of a triangular pyramid are right-angled triangles with right angle vertices at the pyramid vertex. Areas of these sides are
,
and
. Volume of the pyramid (in
) is:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If we were to place the pyramid on the side, we would get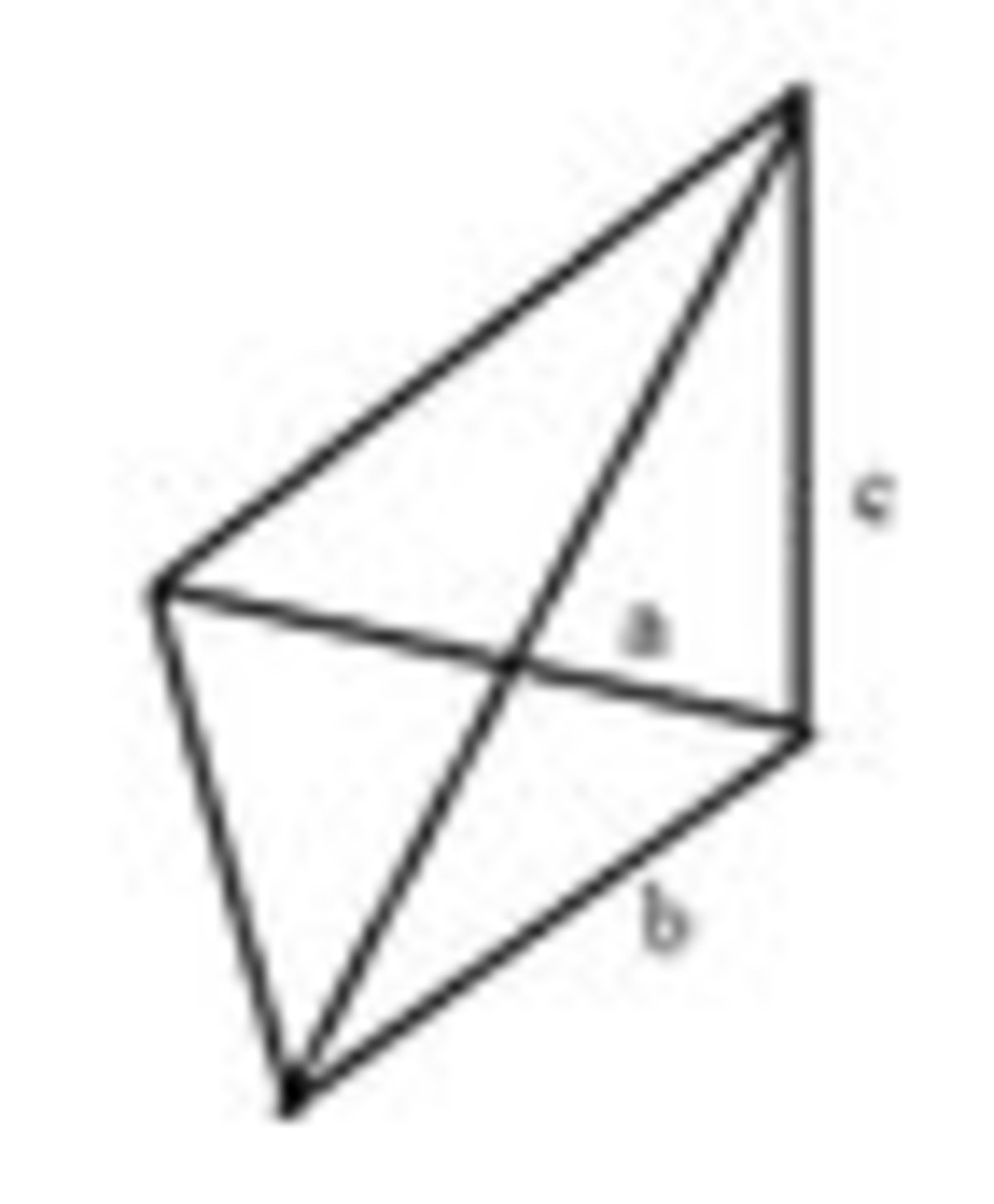 Now we have:
V
=
3
B
H
=
3
2
a
b
×
c
=
6
a
b
c
Now, we know the areas of these sides as:
2
a
b
=
6
c
m
2
2
b
c
=
8
c
m
2
2
a
c
=
1
2
c
m
2
If we multiply these 3 equations we get:
8
a
2
b
2
c
2
=
5
7
6
From there we get
a
b
c
=
4
8
2
, and the volume is
8
2
c
m
3
Now we have:
V
=
3
B
H
=
3
2
a
b
×
c
=
6
a
b
c
Now, we know the areas of these sides as:
2
a
b
=
6
c
m
2
2
b
c
=
8
c
m
2
2
a
c
=
1
2
c
m
2
If we multiply these 3 equations we get:
8
a
2
b
2
c
2
=
5
7
6
From there we get
a
b
c
=
4
8
2
, and the volume is
8
2
c
m
3