Irregularly arranged Regular polygons

Cut up the diagram as follows and swap $A$ with $A'$ and $B$ with $B'$ :

Then $50\% = \boxed{0.5}$ of the octagon is shaded.

Answer to this problem: here For a similar problem, go to this link

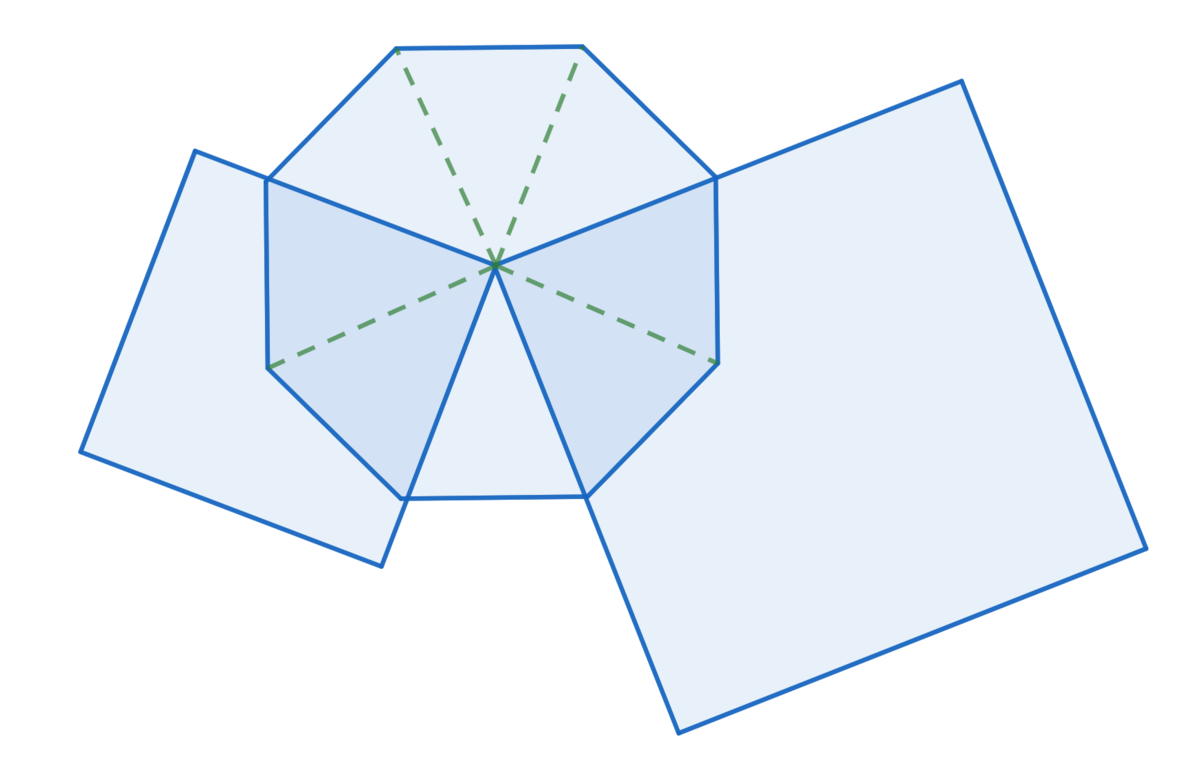
The octagon can be divided into 8 triangles from its centre point. Each triangle has an angle at the centre of $180(8-2)/8 = 45^\circ$ . Each square has an angle at the centre of $90^\circ$ . So if you rotate each square around the vertex at the centre of the octagon until one side of the square crosses a vertex of the octagon, it will cover exactly 2 triangles. Two squares will cover 4 out of the 8 triangles, which is exactly half of the octagon. Therefore the remaining part is also half. $\frac12=\boxed{0.5}$ of the octagon will be shaded.

I just rotated the square on the left until it touched the big square. From there, it is clear that it covers half of the shape.