Is Center of Mass Useful?

Classical Mechanics Level 3

A square wire of side length $L$ and mass $M$ is centered on the origin in the $xy$ plane. A point-particle of mass $M$ is positioned at $(x,y) = (L,0)$ .

What is the magnitude of the gravitational force between the two objects?

Details and assumptions:
1) Everything in standard physical units
2) Gravitational constant $G = 6.67 \times 10^{-11}$
3) $L = 1$
4) $M = 10^6$
5) The wire's mass is uniformly distributed over its length

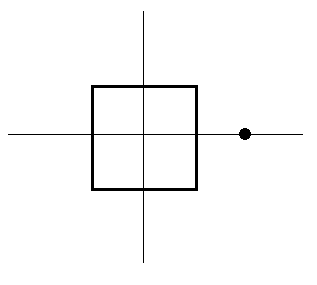
The answer is 80.267.

1 solution

Otto Bretscher
Nov 27, 2018

$\frac{GM^2}{4}\left(\int_{-1/2}^{1/2}\frac{1/2}{(1/4+y^2)^{3/2}}dy+\int_{-1/2}^{1/2}\frac{1/2}{(9/4+y^2)^{3/2}}dy+2\int_{-1/2}^{1/2}\frac{1-x}{(1/4+(1-x)^2)^{3/2}}dx\right)=66.7\left(\sqrt{2}-\frac{2}{3\sqrt{10}}\right)\approx \boxed{80.266}$

With the dimensions of the wire being large relative to the distance of the attracting bodies, naively using the center of mass does not give a good approximation, of course.

Is Center of Mass Useful?

The answer is 80.267.

1 solution

0 pending reports