Is it a segment?
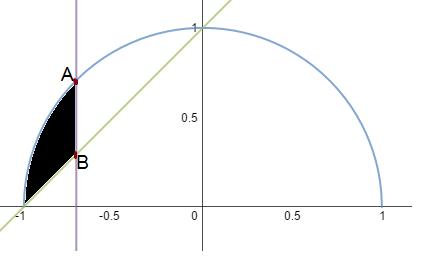 The figure at right shows a unit semicircle (in blue) and the graph of
(in green).
The figure at right shows a unit semicircle (in blue) and the graph of
(in green).
Let the purple line segment be the longest vertical line segment that joins the blue semicircle and green line in the domain
If is the area of the black shaded region, what is
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, to find the x -coordinate that maximizes the length of A B , we need to find which value of x maximizes the length function f ( x ) = 1 − x 2 − ( x + 1 ) , (as the circle has equation x 2 + y 2 = 1 ). Then
f ′ ( x ) = 1 − x 2 − x − 1 = 0 when
− x = 1 − x 2 ⟹ x 2 = 1 − x 2 ⟹ x = − 2 1 ,
as we are clearly looking for a negative x -value. Now f ′ ′ ( x ) = − ( 1 − x 2 ) 2 3 1 < 0 for x = − 2 1 so by the second derivative test we can conclude that the length of A B is maximized for this value of x .
Now define the points P ( − 1 , 0 ) , Q ( − 2 1 ) and O ( 0 , 0 ) . Then the area of the shaded region will be the area of sector A O P minus the combined areas of Δ A O Q and Δ B P Q . Now as 2 1 = cos ( 4 π ) we know that ∠ A O P = 4 π , so the area of sector A O P is just 4 π .
Next, as Δ A O Q and Δ B P Q are both isosceles right triangles, their combined areas will be
2 1 ∗ ( 2 1 ) 2 + 2 1 ( 1 − 2 1 ) 2 = 4 1 + 2 1 ∗ ( 2 3 − 2 ) = 1 − 2 2 .
Thus the area of the shaded region is A = 8 π − 1 + 2 2 = 0 . 0 9 9 8 0 5 8 6 . . . . and so ⌊ 1 0 0 A ⌋ = 9 .