Marbles With An Equal Chance

Lets consider two cases.

1. The first marble is white. Then, the probability of second marble being black, provided first marble is white is given by [ 2/4 * 2/3 = 1/3 ]

2. The first marble is black. Then, the probability of second marble being black, provided first being black is given by [ 2/4 * 1/3 = 1/6 ]

Clearly, the probability of occurrence of first case is more.

[This is not a complete solution.]

This is a common misconception in probability

Supposed that we have events X and Y in chronological order. The outcome of event Y does not affect the outcome of event X. Does knowledge of the outcome of event Y affect the probability of event X's outcome?

This is known as the time-axis fallacy, also called the Falk phenomenon. For those who have solved this problem, please help me write up the misconceptions wiki. Thanks!

Unlike the Monty Hall problem, where the host always shows you one of the two doors containing a goat, his revealing of one of the doors does not affect the odds of your first pick since he purposely avoids showing you which door the car is behind. But, if the door was actually chosen at random, and there was a chance of actually showing you the door which the car was behind, then obviously you'd "swap" to the door with the car if the car was randomly revealed. But, obviously, now that you know where one of the goats are, by "swapping" to another door, you'd have a 50:50 chance of picking the car instead of the 1 in 3 from your initial pick.

In the case of our current problem, the way to calculate the odds is to calculate the permutations of each possible outcome. Let's say Marble 1 is white, Marble 2 is white, Marble 3 is black, and Marble 4 is black:

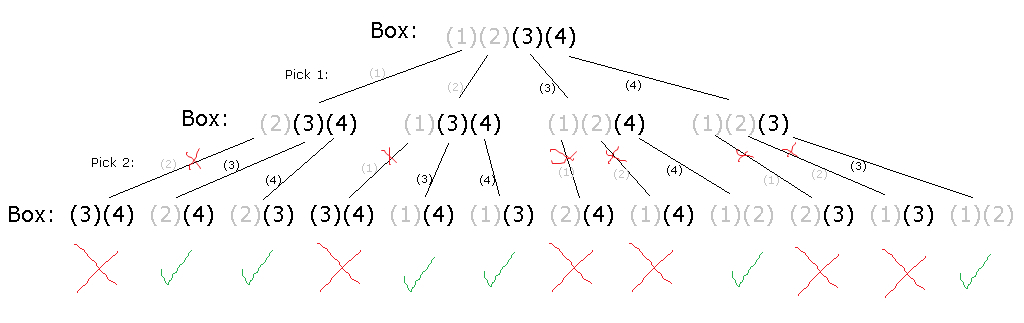
Since we reveal a black marble at the end, there's six trees we can cross out. A better question would be: After we reveal a black marble, what's the odds the first marble we picked is also black? Two of the six remaining trees have 2 white marbles in the box, thus 2 in our hand. So there's a 2 in 6 chance that both marbles we picked are black and a 4 in 6 chance that the first marble we picked is white. Thus the solution to our problem is that our first marble has a greater likelihood of being white because it's double as likely.

We can apply Bayes Theorem to directly calculate the conditional probabilities. Let A denote "First ball is white" and B denote "Second Ball is black".

We are looking for the conditional probability: $P(A|B)$

Clearly $P(A)=\frac{1}{2}$ , and $P(B)=\frac{1}{2}$ , given that there is perfect symmetry, or in other words, as there as many white balls as black balls.

It is simple to determine that $P(B|A)=\frac{2}{3}$ , as after taking a first white ball there remain 2 black balls out of 3.

Now $P(A|B) = \frac{P(B|A)P(A)}{P(B)} = \frac{\frac{2}{3}\frac{1}{2}}{\frac{1}{2}}=\frac{2}{3}$ In other words, knowing that the second ball came out black, it is TWICE as likely that the first had been white than black.

First is more likely to be white

There are 6 possible combination to pull out the marbles:

1 - W W B B

2 - W B W B

3 - W B B W

4 - B W W B

5 - B W B W

6 - B B W W

If second one is black it mean it is part of combination 2,3 or 6:

2 - W B W B

3 - W B B W

6 - B B W W

Meaning that probability that the first one was white were 2 out of 3.

First if I take a white marble, then only 1 white and 2 black marble is left. So, now if I again choose a marble it is more likely than it would be black because of greater number of black marbles.So, as the second outcome is given, we have to choose the option which is opposite to the second outcine ( black) i.e. white

If you select a marble then you take it out of the pot of selection, increasing the odds for the marble color not selected on 1st try to be selected on 2nd try. You have better odds of selecting a black marble the 2nd time if the white marble was selected first, since after that you'll have 2 black marbles to select from against 1 white marble. So it's more likely that the first marble was a white to increase your odds of selecting a black the second time