Is it easy?

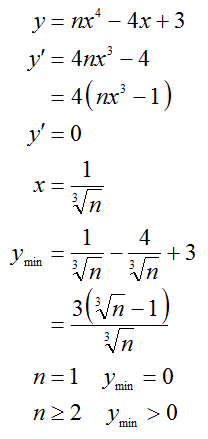
I want to use a little bit calculus here. Let $f(x)=nx^4$ and $g(x)=-4x-3$ . We want $f(x)=g(x)$ has one real solution at least. Note that as $n$ grows graph of $f(x)=nx^ 4$ becomes narrower and it will not touch the $g(x)$ after some $n=n_0$ . So boundary is where $f(x)$ is tangent to $g(x)$ at some point $x=a$ and $n=n_0$ , in other words where $f(a)=g(a)$ and $f'(a)=g'(a)$ or $n_0a^4=-4a-3 \\ 4n_0 a^3=-4$ which gives $a=-1$ and $n_0=1$ . Therefore $n\le n_0=1$ .

Check that $x=0$ is not a solution. $nx^4 + 4x+3=0$ $n=\frac{-4x-3}{x^4} \geq 1$ (Because $n$ is a positive integer) $x^4+4x+3 \leq 0$ $(x^2-1)^2+2(x+1)^2 \leq 0$

So $x=-1$ is the unique solution which occurs when equality above holds i.e. $n=1$ is the only positive integer.

$A=1$ and $S=1$

$A+S=1+1=\boxed{2}$

Slightly Differently

$Let\quad x=\cfrac { -1 }{ y } \quad domain\quad of\quad y\quad is\quad \left( -\infty ,\infty \right) -\left\{ 0 \right\} \\ \\ n=-\cfrac { 4 }{ { x }^{ 3 } } -\cfrac { 3 }{ { x }^{ 4 } } =4{ y }^{ 3 }-3{ y }^{ 4 }=f\left( y \right) \\ \\ \cfrac { dn }{ dy } =12{ y }^{ 2 }\left( 1-y \right) \\ \\ so\quad n=f\left( y \right) \quad increasing\quad for\quad y<1\\ \\ \& \quad decreasing\quad for\quad y>1\\ \\ \Rightarrow { n }_{ max }=f\left( 1 \right) =1\quad so\quad only\quad one\quad +ve\quad integer\quad possible.\\ \\ A+S=1+1=2$