Is it hard?

Classical Mechanics Level 5

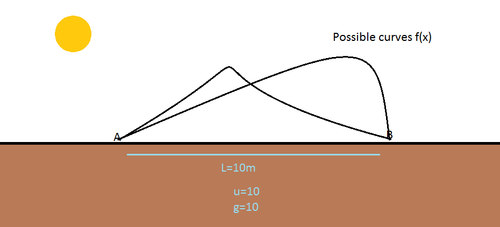Consider all the possible continuous smooth 2-D curves joining two points on the ground ( 'A' and 'B' ) seperatedd by a distance L and lying entirely in the vertical plane,

Let the curve be described as y=f(x) satisfying f'(0)=1
and also as has been mentioned f(0)=f(L)

A particle is to be launched along the curve with an initial speed of u from A, so as to reach at B,

What is the equation of the curve f(x) so that the curve exerts absolutely no Normal reaction upon the particle at each and every point on the curve,

if it can be expressed as

$y=Ax+B{ x }^{ 2 }+C{ x }^{ 3 }+D{ x }^{ 4 }+E{ x }^{ 5 }.......\quad$

Find the sum of the coefficients (algebraic sum , not sum of magnitudes)

Details and Assumptions

1) L= 10

2) g= 10

3) u= 10

3) Neglect buoyancy , viscous drag , size of particle and variation of 'g' with height

(ALL IN SI UNITS)

The answer is 0.9.

2 solutions

Ronak Agarwal
Feb 15, 2015

This question is just too easy since normal at any point is zero hence we can expect the ball to follow it's normal trajectory that is the trajectory of a normal projectile, that is projectile of a parabola.

Hence I would just be writing the equation of trajectory :

$y=xtan(\theta) - \dfrac{g{x}^{2}}{2{u}^{2}cos^{2}(\theta)}$

Put the values to get :

$y=x-\dfrac{{x}^{2}}{10}$

precisely, but it is a fine example of how some IIT problems are designed,

saying f(a)=f(b) and f(x) is one one , inplace of simply telling x=y

Mvs Saketh - 6 years, 3 months ago

exclusively tricky....

Soumya Dubey - 6 years, 3 months ago

Hey Raunak , Can u tell me what u would have done if Normal force would have been given ( as constant or function)

Ayush Choubey - 5 years, 9 months ago

Mayank Singh
Feb 24, 2015

Really, the question was very well framed.

Is it hard?

The answer is 0.9.

2 solutions

0 pending reports