Is it long?
Consider △ A B C having sides A B = A C = 1 4 cm and B C = 2 0 cm .
Let I be the incentre of △ A B C and G be the centroid of the triangle formed by joining the points at which the sides A B , B C and C A are tangent to the incircle of △ A B C .
If I G = c a b cm where g cd ( a , c ) = 1 and b is square-free, then submit your answer as a + b + c .
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
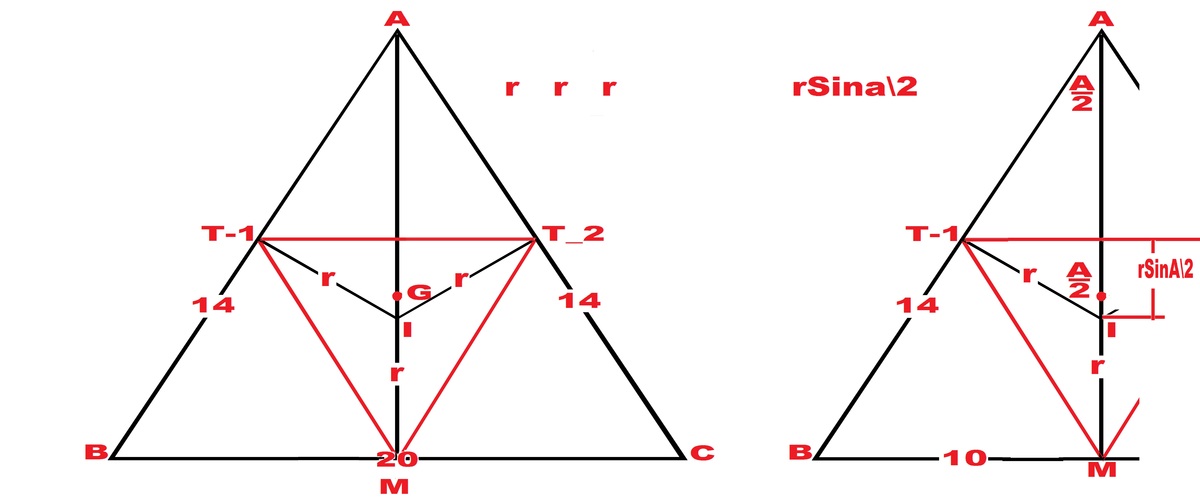 Let M be the midpoint of BC.
∴
A
M
b
y
P
y
t
h
a
g
o
r
a
s
i
s
4
6
.
M
i
s
0
n
e
v
e
r
t
e
x
a
n
d
l
e
t
T
1
,
T
2
b
e
o
t
h
e
r
t
w
o
v
e
r
t
i
c
e
s
o
f
t
h
e
Δ
f
o
r
m
e
d
b
y
t
a
n
g
e
n
c
y
p
o
i
n
t
s
.
I
n
r
a
d
i
u
s
,
r
=
2
1
∗
(
1
4
+
1
4
+
2
0
)
2
1
∗
2
0
∗
4
6
=
3
5
6
.
S
i
n
2
A
=
7
5
.
−
T
1
G
=
+
T
2
G
=
r
∗
S
i
n
2
A
=
7
5
∗
r
.
Let I be the origin of the rectangular coordinate system with AM along X=0.
∴
I
(
0
,
0
)
,
M
(
0
,
−
r
)
,
T
1
(
−
p
,
7
5
∗
r
)
,
T
2
(
+
p
,
7
5
∗
r
)
,
∴
G
⎝
⎜
⎛
3
0
,
3
r
(
−
1
+
7
5
+
7
5
)
⎠
⎟
⎞
=
(
0
,
2
1
5
6
)
.
∴
I
G
=
2
1
5
6
=
c
a
b
.
∴
a
+
b
+
c
=
3
2
Let M be the midpoint of BC.
∴
A
M
b
y
P
y
t
h
a
g
o
r
a
s
i
s
4
6
.
M
i
s
0
n
e
v
e
r
t
e
x
a
n
d
l
e
t
T
1
,
T
2
b
e
o
t
h
e
r
t
w
o
v
e
r
t
i
c
e
s
o
f
t
h
e
Δ
f
o
r
m
e
d
b
y
t
a
n
g
e
n
c
y
p
o
i
n
t
s
.
I
n
r
a
d
i
u
s
,
r
=
2
1
∗
(
1
4
+
1
4
+
2
0
)
2
1
∗
2
0
∗
4
6
=
3
5
6
.
S
i
n
2
A
=
7
5
.
−
T
1
G
=
+
T
2
G
=
r
∗
S
i
n
2
A
=
7
5
∗
r
.
Let I be the origin of the rectangular coordinate system with AM along X=0.
∴
I
(
0
,
0
)
,
M
(
0
,
−
r
)
,
T
1
(
−
p
,
7
5
∗
r
)
,
T
2
(
+
p
,
7
5
∗
r
)
,
∴
G
⎝
⎜
⎛
3
0
,
3
r
(
−
1
+
7
5
+
7
5
)
⎠
⎟
⎞
=
(
0
,
2
1
5
6
)
.
∴
I
G
=
2
1
5
6
=
c
a
b
.
∴
a
+
b
+
c
=
3
2
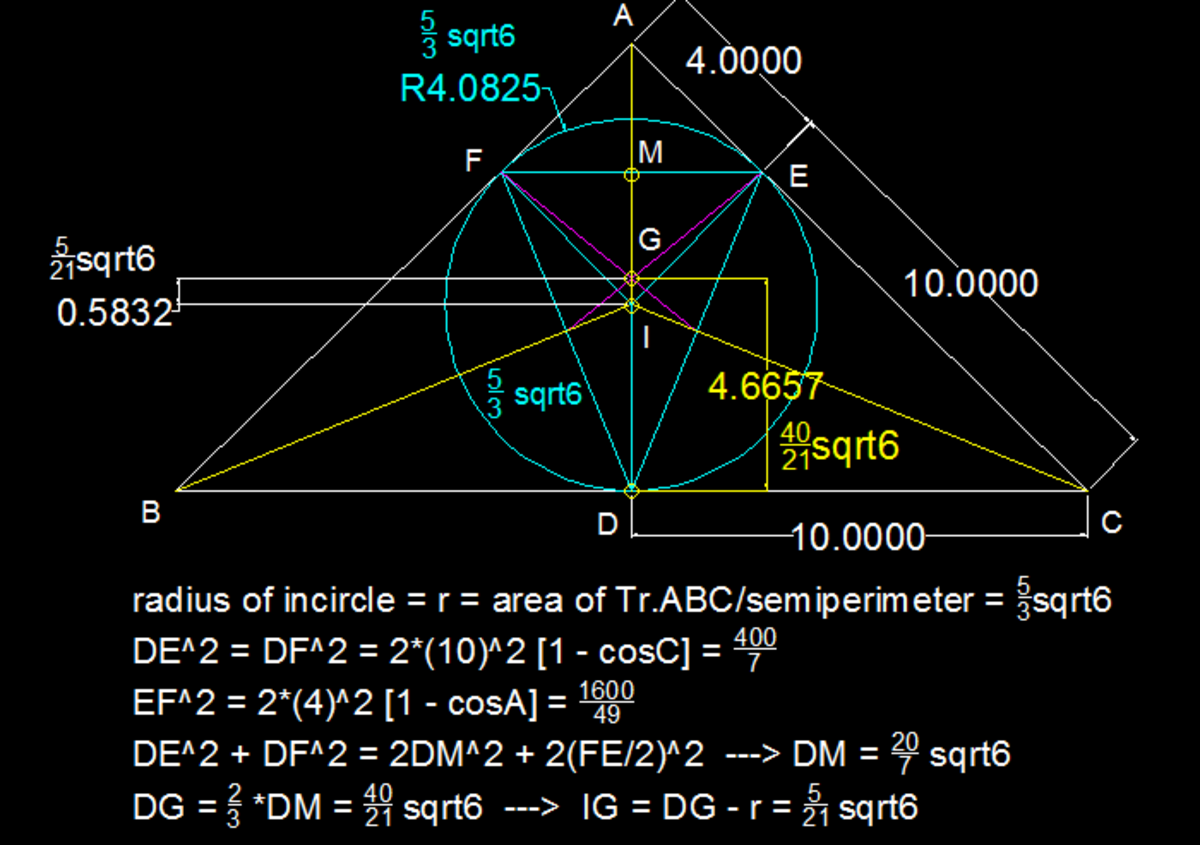
A solution using similarity and Pythagorean Theorem:
Let the midpoint of BC be M. Let the two other points of tangency of the incircle be J and L. Let K be the midpoint of the segment JL.
Note that G,I and M all lie on the perpendicular bisector of △ A B C , so they are collinear.
Let the inradius be r. 2 1 r ( 1 4 + 1 4 + 2 0 ) = A r e a = 2 4 ∗ 1 0 ∗ 1 0 ∗ 4 (using Heron's formula)
Hence r = 3 5 6 .
It is known that the centroid divides a median into 2 segments of ratio 1 : 2 .
A M = 1 4 2 − 1 0 2 = 4 6
Also, △ A B C ∼ △ A J L and J B = B M = 1 0 , so J K = 1 4 4 1 4 4 − 1 0 2 = 7 8 6
Thus G M = 3 2 ∗ ( 4 6 − 7 8 6 ) = 2 1 4 0 6
⇒ I G = G M − I M = 2 1 4 0 6 − 3 5 6 = 2 1 5 6 ⇒ a + b + c = 5 + 6 + 2 1 = 3 2