Is it possible?
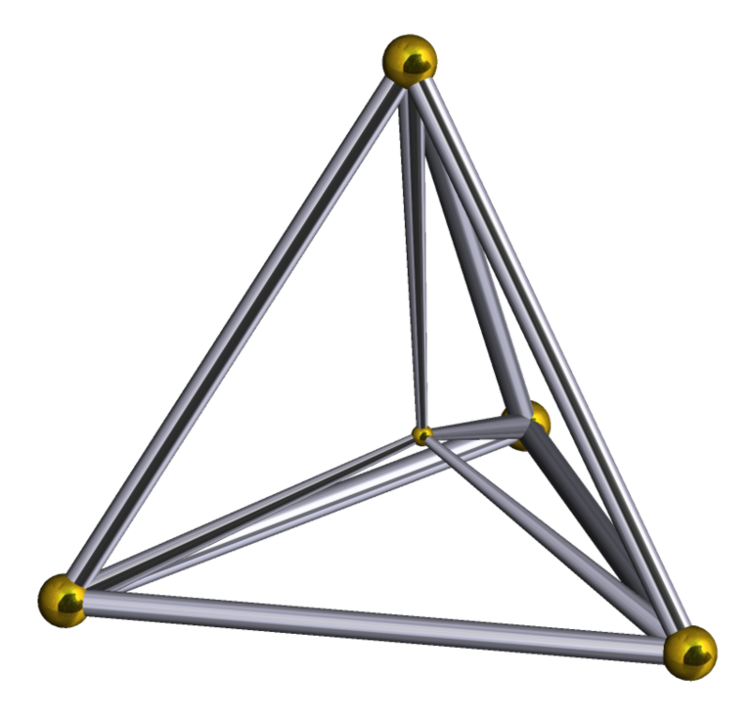 Is it possible to place 5 mutually equidistant points in a 3-dimensional space?
Is it possible to place 5 mutually equidistant points in a 3-dimensional space?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Indeed! Could you share an explanation of why this is true?
Log in to reply
Suppose you have k + 1 points. Make your axes such that one of the points is on the origin and represent the other points with the vectors v 1 , . . . , v k . We shall show that for all k + 1 points to be equidistant to each other, we must have that the vectors v i must all be linearly independent and therefore the dimension must be at least k .
Let the common distance between the points be d . Since all the points are equidistant to each other, we have that
∣ ∣ v i ∣ ∣ 2 = d 2
and
∣ ∣ v i − v j ∣ ∣ 2 = d 2
for all i = j . Expanding the second equation we get
∣ ∣ v i ∣ ∣ 2 + ∣ ∣ v j ∣ ∣ 2 − 2 v i ⋅ v j = d 2
and plugging in the first equation we get the result
v i ⋅ v j = 2 d 2 .
Now assume for the sake of contradiction that the vectors are not linearly independent and order them in such a way that you have
v k = ∑ i = 1 k − 1 a i v i .
Also, let
C = 2 d 2 ∑ i = 1 k − 1 a i .
Now we try to see how these constraints affect the coefficients of v k . Computing the dot product we get
v k ⋅ v j = C + 2 d 2 a j
by distributing the dot product though the sum and using the equations for length and dot product above. This dot product also has to equal 2 d 2 for all j , so in particular for j = j ′ , we must have that
C + 2 d 2 a j = C + 2 d 2 a j ′
⇒ a i = a j ′ .
Solving for the coefficients yields
v k = k 1 ∑ i = 1 k − 1 v i .
However, this implies that
∣ ∣ v k ∣ ∣ 2 = k 2 1 ( ( k − 1 ) d 2 + ( k − 1 ) ( k − 2 ) 2 d 2 ) = d 2 ⋅ 2 k k − 1 < d 2
which is a contradiction! Therefore we must have that in n dimensions at most n + 1 points can be equidistant from each other.
Afternote: We gave an upper bound on the number of points allowed, but it turns out that this bound is tight because you can build up a set of n + 1 equidistant points in n dimensions in the following way. For simplicity, let the common distance be 1. Start with the origin. Suppose you have done this process for the first k − 1 dimensions and have built up k points (including the origin) that are equidistant and only have non-zero coordinates in the first k − 1 dimensions. Let v k = k 1 ∑ i = 1 k − 1 v i + 1 − 2 k k − 1 e k , where e k is a unit vector in the k th dimension. This new vector is equidistant from all the other vectors (because it is the same as the construction above with an extra term that is perpendicular to every other vector so it doesn't change the dot products), and it is also the right distance away from the origin because that's how the coefficient of the last term was selected. Therefore we keep doing this process and will eventually get a set of n + 1 points in n dimensions that are equidistant from each other.
Its easy to look on nature. No structures of chemistry contains this. So its impossible.
A maximum of n+1 mutually equidistant objects can be placed in a n-dimensional space.