Is it possible?
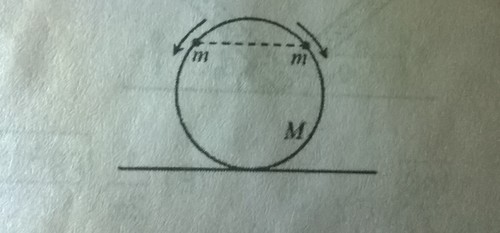 Two beads of mass
each are positioned at the top of a frictionless hoop of mass
with radius
, which stands vertically on the ground. The beads are given a slight push, and they slide down the hoop, one to the right and the other one to the left, as shown . What is the smallest value of
for which the hoop will rise up off the ground at some time during the motion?
Two beads of mass
each are positioned at the top of a frictionless hoop of mass
with radius
, which stands vertically on the ground. The beads are given a slight push, and they slide down the hoop, one to the right and the other one to the left, as shown . What is the smallest value of
for which the hoop will rise up off the ground at some time during the motion?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From symmetry we can say that both the beads at any instant will make equal angle the vertical.
Draw the FBD of any bead when it makes angle θ with the vertical. In the diagram assume that ring provides normal force ( N ) towards the center to the bead(and not away from the center).
Taking radial acceleration of the bead to be 0 we can write that m g cos θ + N = R m v 2 By conservation of energy we can write that:- 2 1 m v 2 = m g R ( 1 − cos θ ) v = 2 g R ( 1 − cos θ ) From the previous eqaution we can write that:- N + m g cos θ = R m . 2 g R ( 1 − cos θ ) N = 2 m g − 3 m g cos θ This is the same force which the bead is providing to the ring in the direction making angle θ with the ring.
Let total force provided by the beads is F n e t . F n e t = 2 N cos θ F n e t = 2 ( 2 m g − 3 m g cos θ ) cos θ F n e t = 2 m g ( 2 − 3 cos θ ) cos θ For Maximum F n e t :- ( ( 2 − 3 cos θ ) cos θ ) ′ = 0 cos θ = 3 1 Hence:- F n e t = 3 2 m g This force should be equal to M g to lift the ring:- 3 2 m g = M g M m = 2 3