Is It Possible

Logic Level 1

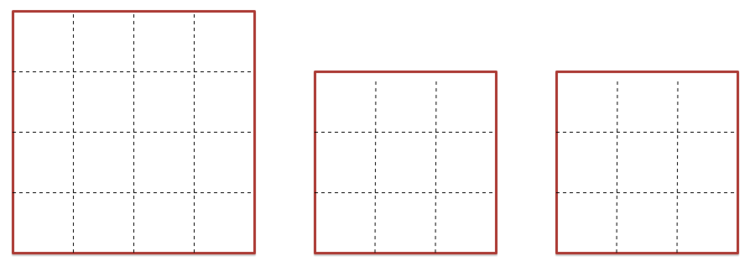I have 3 transparent squares. The two smaller squares are identical and their sides are 3/4 the size of the sides of the large square.

Is it possible to place these squares together in a way that will result in a figure that displays six squares (of any size)?

No Yes

Aman Baser by Aman Baser , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Aman Baser
Jun 11, 2015

Here's one way.

26 Helpful 0 Interesting 0 Brilliant 0 Confused

How did you approached? Can you share please

sandeep Rathod - 5 years, 12 months ago

Thought of the same thing but missed the two corner ones...

Hon Ming Rou - 5 years, 12 months ago

How come? You said they were transparent. How can they be superimposed over each other? You would get only transparency!!!

Karthik Sekaran - 5 years, 4 months ago

This question is poorly formed. It does not specify whether the squares should be overlaid, or must be tiled. It does not specify that the squares must formed exclusively from the edges of the squares. I was working the problem of how many imaginary squares could be formed from tiled squares.

Ted Schober - 5 years, 4 months ago

Log in to reply

YES IT IS TRUE

Pranshu Aggarwal - 5 years, 4 months ago
Sravanth C.
Jun 21, 2015

Here's another way.

5 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Typically for such problems, you should target exactly what is stated. Of course, there is ambiguity in what is allowed / disallowed, to avoid a tedious question.

This solution displays 8 squares

Andrés Lucena - 5 years, 11 months ago

Log in to reply

Yeah. But it's not mentioned in the question that we need to get exactly 6 6 squares. . .

Sravanth C. - 5 years, 11 months ago

Hmm, looks like 8 squares than 6... if counting the 4x4 squares in the middle. The top (big square's bottom right corner), and the bottom (3/4 square's top left corner).

Edward Balaoro - 5 years, 11 months ago
Dori Deng
Jun 22, 2015

Here's another answer

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Ayushmaan Sharma
Jun 21, 2015

well this solution will sound funny but if we will imagine the inside square as 1cm(any value can be imagined) then smaller square upon larger square will result 3upon4

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...