Appearances are sometimes deceiving
A triangle's angles are:
,
, and
. We drop perpendiculars from the midpoints of the sides as is shown the figure below.
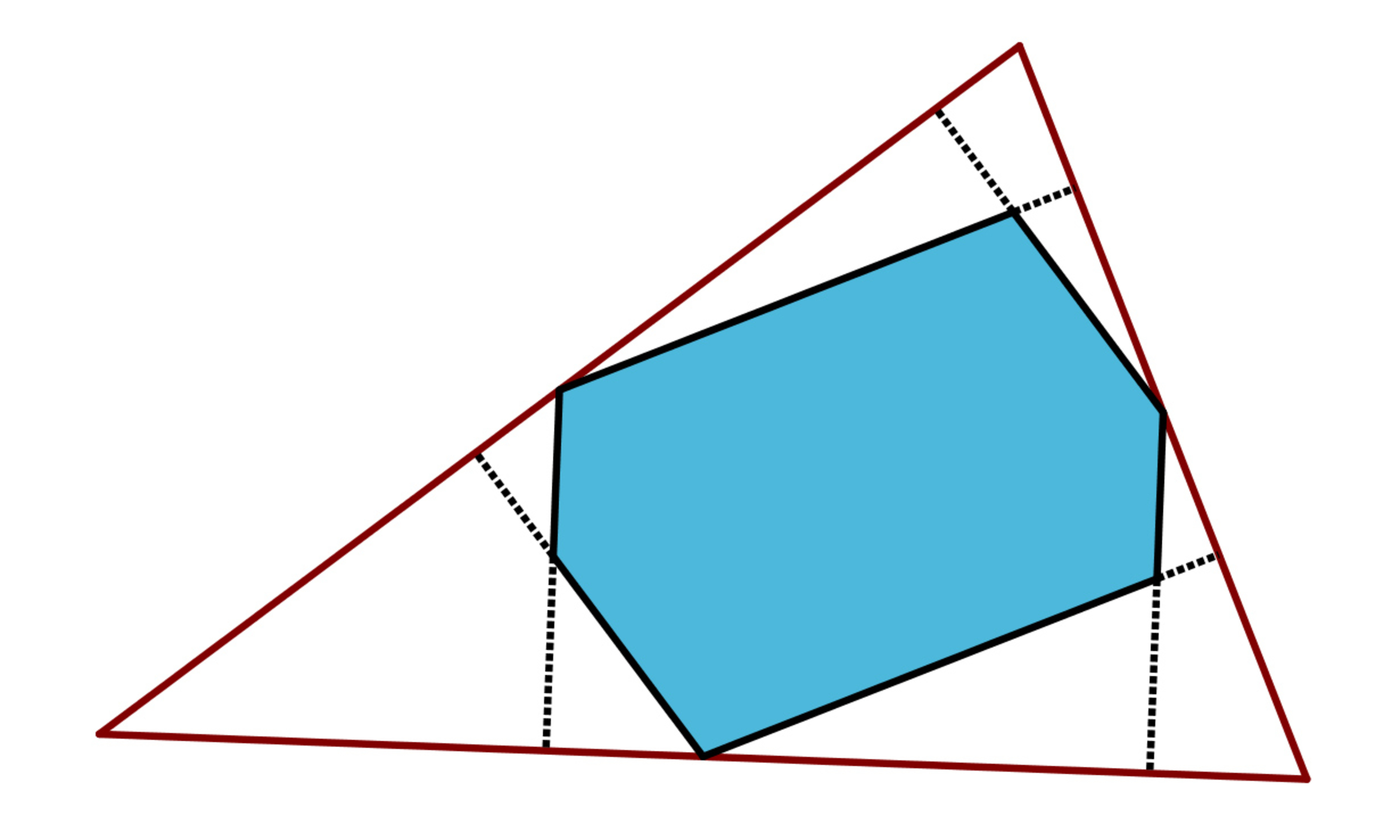
If the area of the blue hexagon is , and the area of the triangle is , then find the value of .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Note:
1) All vertices of the hexagon lie on the nine-point circle of the large triangle.
2) The ratio is the same regardless of the angle measures.