Is it safe to go?
Imagine you are a Galvanian creature in the exoplanet of Galvan. This planet is known for its frequent quakes and how they have terrified the Galvanian civilization for millions of years. The first few thinkers decided they would study their planet to see if they could figure out a model to predict the quakes, but they did so in vane: it seemed like they were completely random. However, they could constantly observe two things: a quake will
ALWAYS
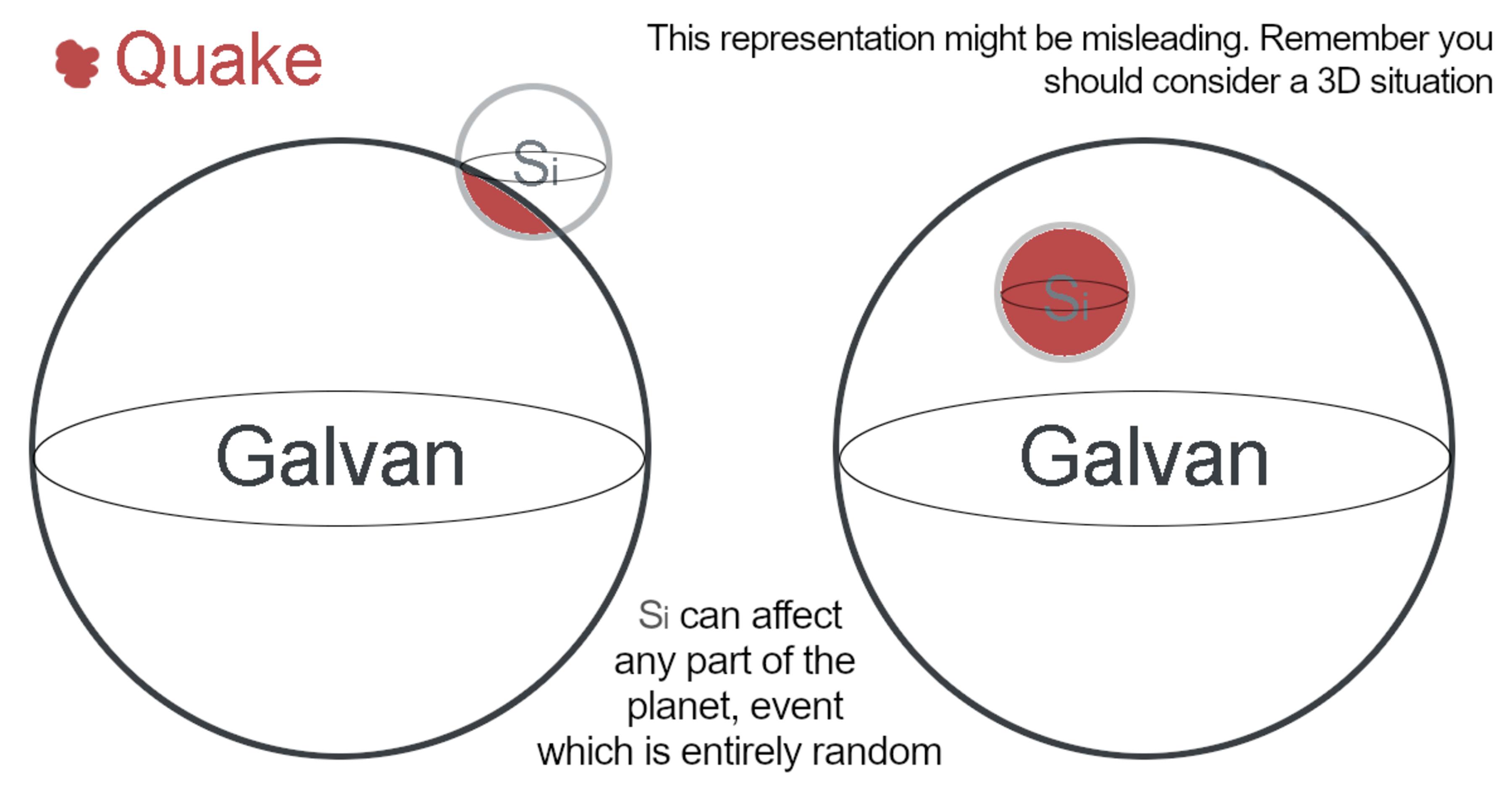
happen in a cycle (where a cycle lasts half a day), even if it's imperceptible, and the biggest quakes affect a spherical space about 125 times smaller than their planet and only happen underground. With this information, they created a probabilistic model which basically consists in a imaginary sphere
, with constant radius, that will "appear" in a random position in space at any moment in a cycle. The region where this imaginary sphere intersects with the planet is where the quake will happen. Strangely, this model works well.
You want to get where your good friend Mike is, to spend the vacations, but you're afraid of the quakes. The distance you need to travel is 12,000 km which requires you to travel in your fastest ground-vehicle, which runs up to 220 km/h.
- What is the probability that in your trip you won't run into a quake? Express your answer in percentage and truncate it to the first three decimal digits.
Details and assumptions
- Assume quakes only happen at the intersections, they don't spread further.
- It will be a non-stop trip at a constant speed.
- A Galvanian day is 20 hours.
The answer is 97.254.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The first thing we can deduct is that the radius of S i is equal to 5 r , where r is the radius of Galvan. This is because the biggest quakes will occur only when S i is completely buried buried under the surface of Galvan, as shown in the diagram above. Comparing volumes:
V Galvan = 3 4 π r 3 , V S i = 3 4 π ( 5 r ) 3 = 3 4 π r 3 ⋅ 1 2 5 1
Now, to calculate the probability we have to change our way to think about the problem a bit, since thinking in terms of a complete sphere S i is hard. Instead, it is easier to think about points and lines , zero and one-dimensional objects, rather than objects in higher dimensions. So we'll call the center of S i a point C i . We know that a point P is affected by a quake if it is within the radius of S i , which is to say that P is a distance d away from C i , where 0 < d < 5 r .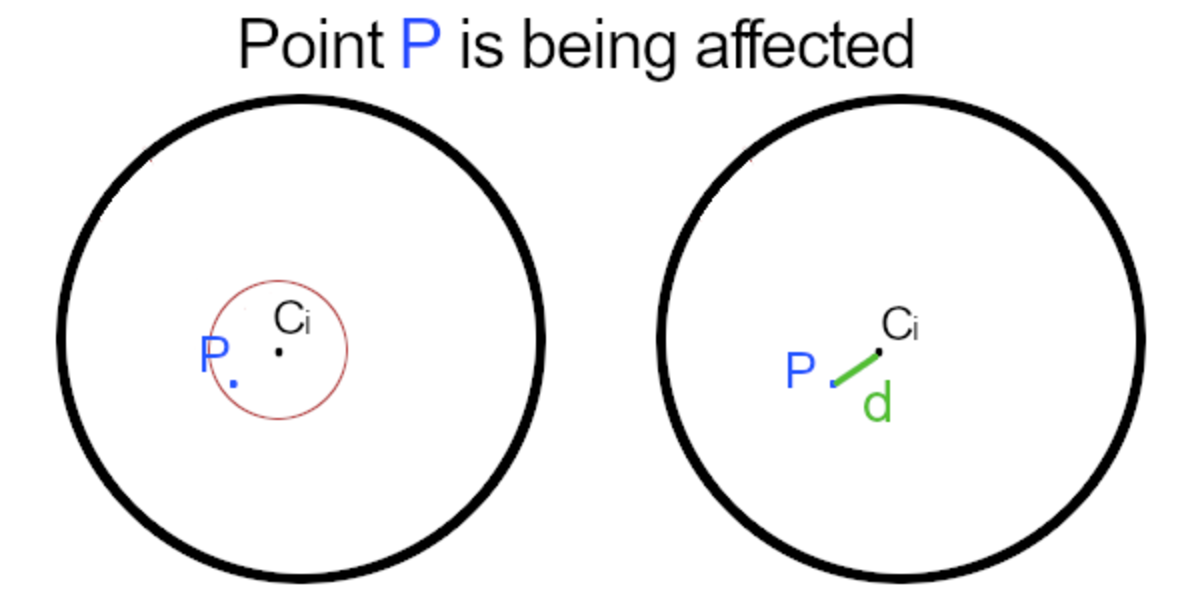 Now, we know that the probability of a point randomly appearing within a certain expected space, which we'll call
S
expected
, is given by the quotient of
S
expected
and the total space where the point can appear,
S
total
:
Now, we know that the probability of a point randomly appearing within a certain expected space, which we'll call
S
expected
, is given by the quotient of
S
expected
and the total space where the point can appear,
S
total
:
P ( X ) = S total S expected .
It is clear that S total cannot be the infinitely vast space, because if S total → ∞ ⟹ P ( X ) → 0 , and clearly this is not true; it is an event that has been happening for years, and somehow this probabilistic model explains it successfully. Notice that if C i appears inside Galvan, then a quake will happen because an intersection is guaranteed. However, outside Galvan C i is limited to appear a distance d away from the surface of the planet, where 0 < d < 5 r , because there cannot exist a cycle where a quake doesn't happen; with this boundary we ensure that stays true.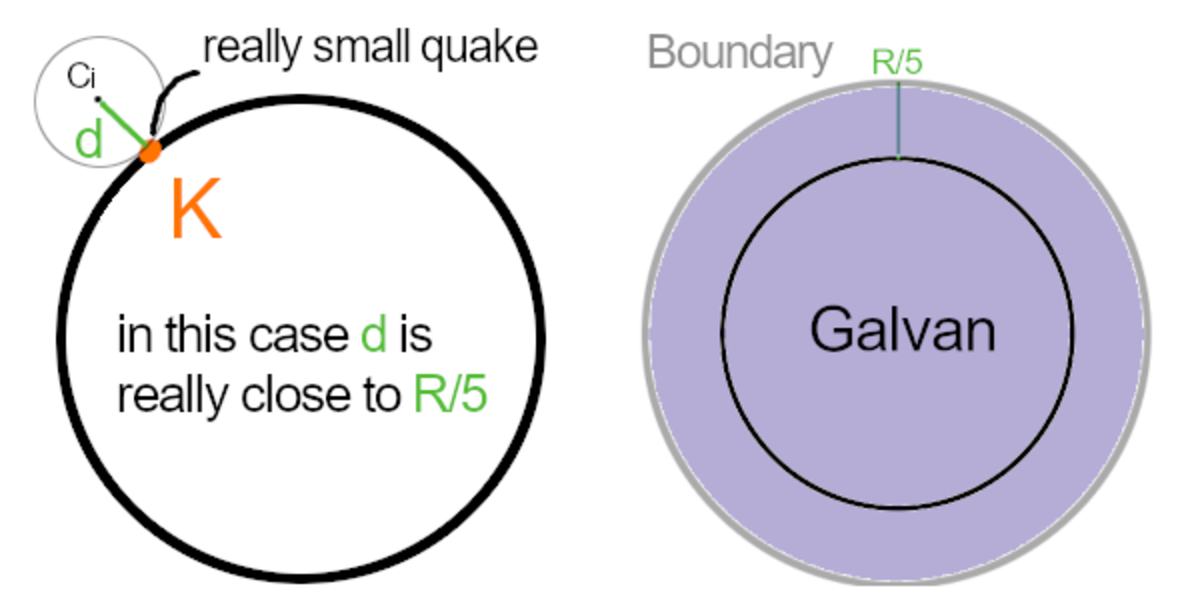 Calculating
S
total
is calculating the volume of the sphere of radius
r
+
5
r
=
5
6
r
:
Calculating
S
total
is calculating the volume of the sphere of radius
r
+
5
r
=
5
6
r
:
S total = 3 4 π ( 5 6 r ) 3 = 1 2 5 2 8 8 π r 3
To calculate S expected , we'll first calculate the probability of getting hit by a quake, plug it into the formula for P ( X ) , and subtract that from 1, as it is easier that way. Consider you are located at a point K . Then, if C i appears within a spherical "aura" of radius 5 r centered at K , you will feel a quake.
So the probability of getting hit by a quake is given by:
P ( Q ) = S total S expected = 3 7 5 4 π r 3 ⋅ 2 8 8 π r 3 1 2 5 = 2 1 6 1 ≈ 0 . 4 6 2 % (This works because even though you are in motion, travelling to Mike, at every instance in time you will find yourself at some point K )
Here we can quickly see that the probability of NOT getting hit by a quake is 1 − P ( Q ) = 2 1 6 2 1 5 ≈ 9 9 . 5 3 7 % .
Finally, to calculate the probability of reaching Mike without running into a quake, we need to know how many cycles are we going to go through, since one quake always happens each cycle. Dividing the distance we need to travel by our speed will give us the time it will take us, and since a single a cycle is 10 hours long, dividing by 10 is how many cycles we'll go through:
Cycles = 2 2 0 h km 1 2 0 0 0 km ⋅ 1 0 h 1 = 1 1 6 0 ≈ 5 . 4 6
This number is greater than 5, so we are going through 6 cycles, which is, 6 times the event needs to repeat. So the final answer is:
( 1 − P ( Q ) ) 6 = ( 2 1 6 2 1 5 ) 6 ≈ 9 7 . 2 5 4 %
Which I think is safe enough for Galvanian standards.