Is It A Square?
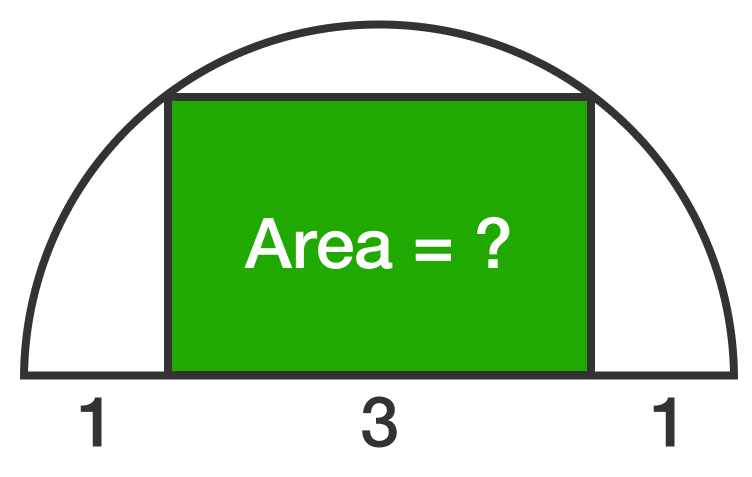
In the above semicircle, we mark off lengths of 1, 3 and 1 along the diameter. We then draw a rectangle on side length 3, till it touches the semicircle
What is the area of the green rectangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Good explanation. Also your diagram is very clear. What tool did you use to draw it?
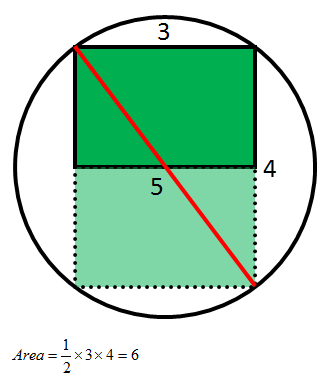
I think the problem has bad multiple choices. without trying to solve the problem first, I know that the triangle area is 6 (without knowing why). Maybe, you could change them to multiplication of 3.
In the top right of the diagram, it should be |BC|=1.5 or |BD|=3 ...... NOT |BC|=3
Log in to reply
I have fixed the diagram! Thanks for catching the typo! :)
cool I couldn't figure this one out
Log in to reply
..and now you know how to work out this problem! :)
Oh, very nice flipping!
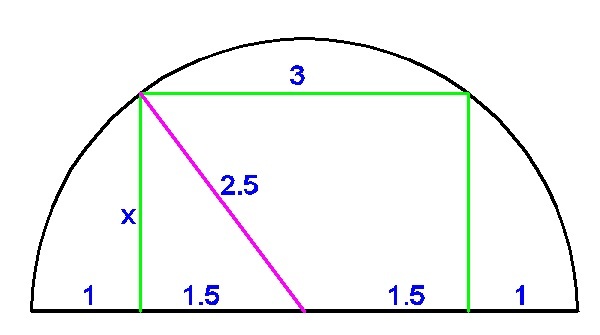
x = 2 . 5 2 − 1 . 5 2 = 2 u n i t s
a r e a = 2 ( 3 ) = 6 s q u a r e u n i t s
The vertical side of the rectangle is essentially the geometric mean of two numbers: 1 and 3 +1 = 4 ie. the square root of 1 x 4 = 2.
It follows that the areas of the rectangle is therefore 2 x 3 = 6
Oh, that's a quick trick to find the vertical side of the rectangle using power of a point . Very nice :)
Can you explain why the vertical line should be the geometric mean of these two lengths? I also cannot see how this relates to the power of a point...
Log in to reply
Look at this http://www.cut-the-knot.org/pythagoras/GeometricMean.shtml
and this: https://en.wikipedia.org/wiki/Semicircle
You can derive this yourself with elementary applications of Pythagoras theorem.
It's only known as the 2 secant theorem, which says that if AB and CD are chords of a circle that intersect at P, then P A × P B = P C × P D .
So, in this problem, we take A B to be the diameter of the semicircle, and C D to be the vertical line (but remember that we need a circle and not a semicircle). So, point P because the left corner of the rectangle, and we get P A × P B = 1 × 4 .
diameter is 5. Hence radius is 2.5
Now from centre to one edge of the rectangle forms a right triangle with H=2.5 with B=1.5. So P=2. Area is 3*2
Pythagoras theorem to the rescue!
Add 1+3+1=5 the diameter of the circle. Thus 2.5 is the radius. Half of 3 is 1.5. Now a right triangle measuring 1.5 on one leg and 2.5 on the Hypotenuse is formed. Noticing a pattern, multiply by 10 and divide by 5 reveals a 3-4-5 right triangle. Thus 4×5/10=2. 2×3=6 the area of the rectangle.
Here is the following illustration as the start: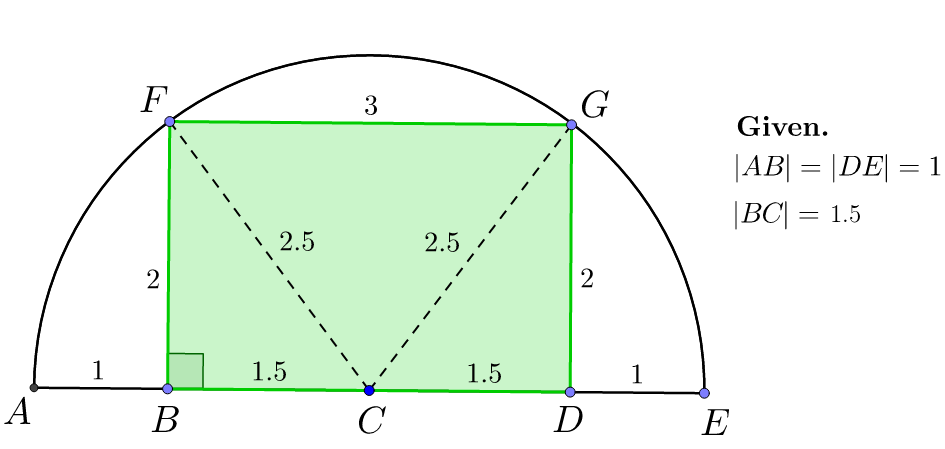
Because of line length symmetry for A E , we can conclude that ∣ A C ∣ = 2 . 5 , which is the radius of the semicircle. Thereby, ∣ F C ∣ = ∣ G C ∣ = 2 . 5 .
Because of midpoint C , we see that ∣ B C ∣ = ∣ A C ∣ − ∣ A B ∣ = 1 . 5 and also ∣ C D ∣ = ∣ C E ∣ − ∣ D E ∣ = 1 . 5 . Since Δ B F C is the right triangle (as well as Δ C G D ), Pythagorean theorem shows that ∣ F B ∣ 2 + ∣ B C ∣ 2 ∣ F B ∣ = ∣ F C ∣ 2 = ∣ F C ∣ 2 − ∣ B C ∣ 2 = 2 which thus shows that the area of the rectangle is A = ∣ F B ∣ × ∣ B D ∣ = 6 .