Is Thales' Theorem Necessary?

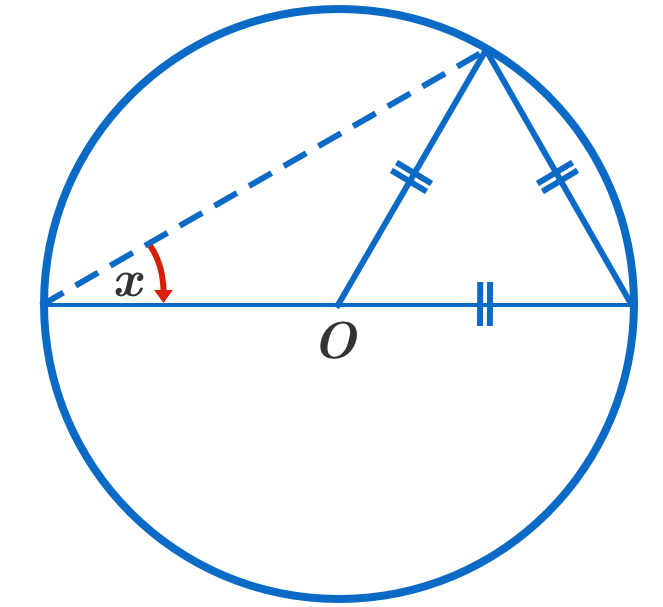
Let us label the points $O, P, Q$ and $R$ as shown in the figure.

Since the triangle $OQR$ is an equilateral triangle, then each of its interior angles must be equal, so $\angle QOR = \dfrac{180^\circ}3 = 60^\circ$ .

And because $POR$ is a straight line, then $\angle POQ = 180^\circ - \angle QOR = 180^\circ = 120^\circ$ .

Notice that both the distances $PO$ and $OQ$ represents the radius of the circle, thus $PO = OQ$ , and so $\triangle POQ$ is an isosceles triangle.

We have $x = \angle PQO = \angle QPO = \dfrac12(180^\circ - 120^\circ) = \boxed{30^\circ}$ .

Relevant wiki: Thales' Theorem

The angles of the big triangle are 90 degrees(angle subtended at circumference by diameter),60 degrees and x degrees. Therefore x is 30 degrees.

We use the rule that the angle subtending a chord made at the centre is twice that of the angle at the circumference. The angle at the centre is $60^{\circ}$ , so the angle at the circumference is $30^{\circ}$ .

180 divded by 3 is 60 so 60 plus 30 is equal to 150 180 -150 =30