Is the Given Information Sufficient?

For my Solution One must needed to know some physics !!

So Put the Point masses at the various points .

Put mass 3 kg at C and now using the concept that mass moment about the centre of mass of an system are equal so at point E we must have to put mass of 10 kg

So Mass at the COM of CE is 13 kg which is present at the point O

Similarly at point 'A' mass would be 4 kg and at the point 'D' it is 9 kg

So by equating mass moment about point 'E'

$BE\quad \times \quad 6\quad =\quad EA\quad \times \quad 4\\ \\ \cfrac { BE }{ EA } \quad =\quad \cfrac { 4 }{ 6 } \quad \quad \quad \quad .\quad .\quad .\quad .\quad \quad (1)$ .

And by equating mass moment about point 'D'

$BD\quad \times \quad 6\quad =\quad DC\quad \times \quad 3\\ \\ \cfrac { BD }{ CD } \quad =\quad \cfrac { 3 }{ 6 } \quad \quad \quad \quad .\quad .\quad .\quad .\quad \quad (2)$ .

By adding 1 and 2 we get

$\\ \cfrac { BD }{ CD } \quad +\quad \cfrac { BE }{ EA } \quad =\quad \cfrac { 7 }{ 6 }$ .

$m = 7$ .

$n= 6$ .

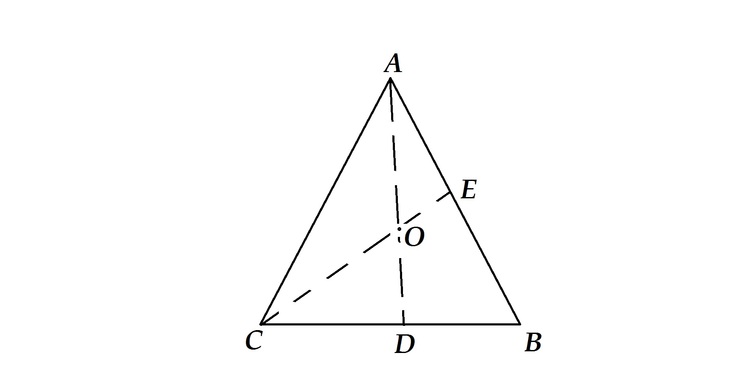Let the areas of $\triangle ACO, \triangle AEO, \triangle EBO, \triangle BDO$ and $\triangle CDO$ be $a,b,c,d$ and $e$ respectively. Then we have:

$\dfrac {a}{b}= \dfrac {OC}{OE}=\dfrac {10}{3}\quad \Rightarrow b = \frac {3} {10} a\quad ...1$

$\dfrac {d+e}{c}= \dfrac {OC}{OE}=\dfrac {10}{3}\quad \Rightarrow d+e - \frac {10} {3} c=0\quad ...2$

$\dfrac {a}{e}= \dfrac {OA}{OD}=\dfrac {9}{4}\quad \Rightarrow e = \frac {4} {9} a\quad ...3$

$\dfrac {b+c}{d}= \dfrac {OA}{OD}=\dfrac {9}{4}\quad \Rightarrow b+c - \frac {9} {4} d=0\quad ...4$

Substituting eq. 3 in eq. 2 and multiplying throughout by $\frac {9}{4}$ :

$\Rightarrow \frac {9}{4}d+\frac {9}{4}\frac {4}{9}a - \frac {9}{4}\frac {10} {3} c=0\quad \Rightarrow \frac {9}{4}d+a - \frac {15}{2}c=0 \quad ...5$

Substituting eq. 1 in eq. 4:

$\Rightarrow \frac {3} {10} a+c - \frac {9} {4} d=0\quad ...6$

Adding eq. 5 to eq. 6 $\Rightarrow \frac {13} {10} a - \frac {13}{2})c = 0 \quad \Rightarrow c = \frac {1}{5}a$

Substituting $c = \frac {1}{5}a$ in eq. 5:

$\Rightarrow \frac {9}{4}d+a - \frac {15}{2}\frac {1}{5}a=0\quad \Rightarrow d = \frac {2}{9}a$

Now we have: $\dfrac {BE}{EA} + \dfrac {BD}{DC} = \dfrac {c}{b} + \dfrac {d}{e} = \frac{1}{5} \times \frac{10}{3}+\frac{2}{9} \times \frac{9}{4} = \frac{2}{3} + \frac{1}{2} = \frac{7}{6} = \dfrac{m}{n}$

Therefore, the required answer $m+n-2=7+6-2=\boxed{11}$

Join BO and extend it to F on AC.

Now, I don't know how to prove it and I want proof of it too(maybe it needs mass point geometry or it can be done using Ceva's theorem too I guess.)

$\frac{OD}{AD} + \frac{OE}{CE} + \frac{OF}{BF} = 1$

$\frac{3}{13} + \frac{4}{13} + \frac{OF}{BF} = 1$

$\frac{OF}{BF} = \frac{6}{13}$

$\frac{OB}{OF} = \frac{7}{6}$

Also, I saw the following somewhere(Wikipedia though) and want to know its proof

$\frac{BO}{OF} = \frac{BE}{EA} + \frac{BD}{DC}$

Hence, $\frac{BE}{EA} + \frac{BD}{DC} = \frac{7}{6}$

Cevas theorem apply to the triangle BCE and vertices A,O,D,and once more Cevas theroem aplied to the triangle DBA and vertices A,O,D gives solution after minut or two calculating...