Is the information sufficient 8?
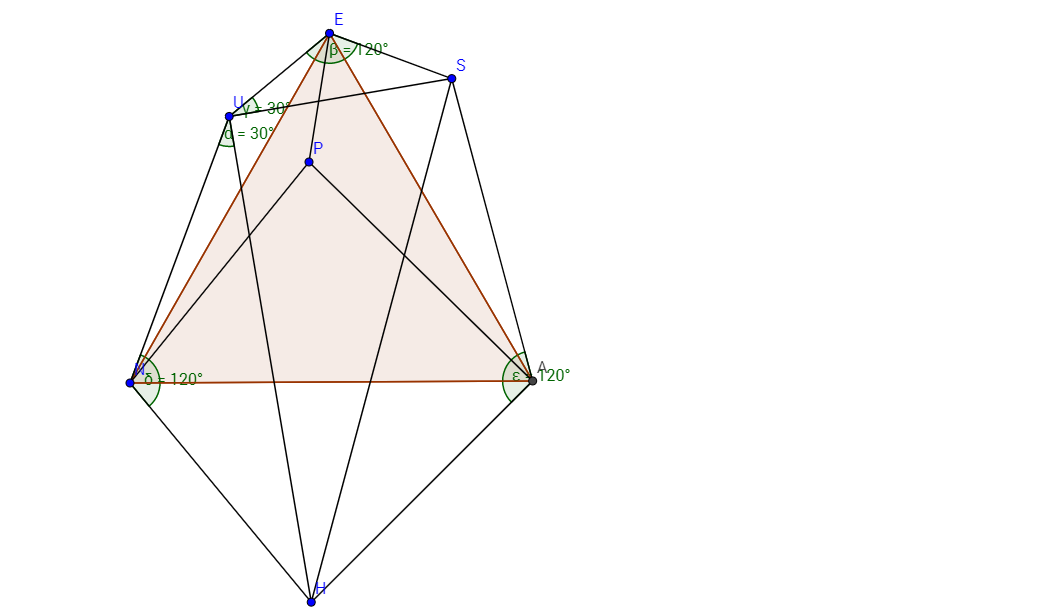
You have a Hexagon, named EUNHA S . Also, you are given that:
- m ( E U ) = m ( E S ) = 1 9
- m ( U N ) = m ( N H ) = 1 8 0
- m ( H A ) = m ( A S ) = 1 8 1
- m ( ∠ U E S ) = m ( ∠ U N H ) = m ( ∠ H A S ) = 1 2 0 ∘ ⋅
If the value of ( m ( E A ) ) 2 can be express as a + b c where c is a prime, what is the value of ⌊ a + b + c ⌋ ?
Clarification:
m ( A X ) means the length or measurement of line segment A X for example, while m ( ∠ R E S ) means the measurement of angle R E S ⋅
For more problems like this, try answering this set .
The answer is 190.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The problem came from this.
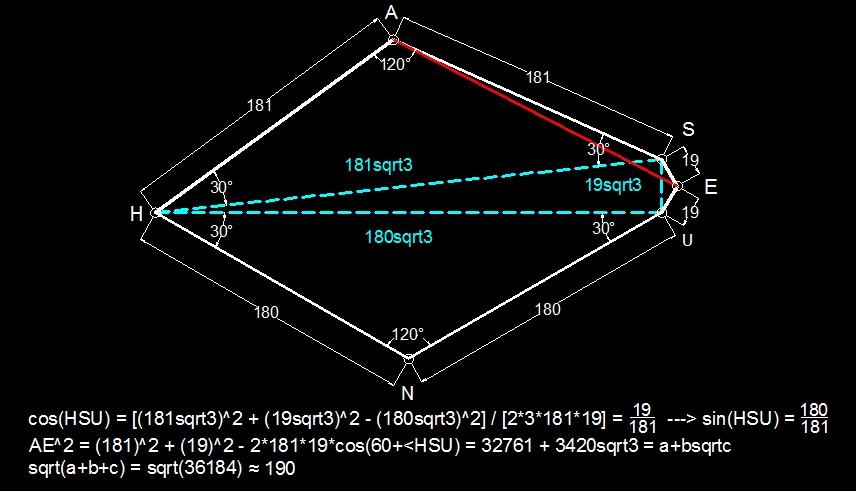
Consider an equilateral triangle E N A , with a point P located inside that triangle such that, E P = 1 9 , P N = 1 8 0 , P A = 1 8 1 ⋅
Now, reflect point P with respect to line segment E N . Let's name the point of reflection U ⋅
So, we can conclude that: E U = 1 9 , U N = 1 8 0 ⋅
Next, reflect point P again, this time respect to line segment E A . Let's name the point of reflection S ⋅
Again, we can conclude that: E S = 1 9 , S A = 1 8 1 ⋅
Lastly, reflect point P with respect to line segment A N . Let's name the point of reflection H ⋅
So, we can conclude that H N = 1 8 0 , H A = 1 8 1 ⋅
It is left to the readers how m ( ∠ U E S ) = m ( ∠ U N H ) = m ( ∠ H A S ) = 1 2 0 ∘ ⋅
Connecting the 6 points will give us the Hexagon, named EUNHA S .
As △ E U S is isosceles, ⟹ ∠ E U S = 3 0 ∘
As △ U N H is isosceles, ⟹ ∠ N U H = 3 0 ∘
As △ S U H is right (right-angled at U ), ⟹ ∠ E U N = 3 0 ∘ + 3 0 ∘ + 9 0 ∘ = 1 5 0 ∘ ⋅
As the quadrilateral E U N P is a kite, ⟹ ∠ E P N = 1 5 0 ∘ ⋅
and therefore,
( m ( E A ) ) 2 = ( m ( E N ) ) 2 = 1 9 2 + 1 8 0 2 − 2 ( 1 9 ) ( 1 8 0 ) ( cos ( 1 5 0 ∘ ) ) = 3 2 7 6 1 + 3 4 2 0 3 = a + b c ⟹ a = 3 2 7 6 1 , b = 3 4 2 0 , c = 3 ⟹ ⌊ a + b + c ⌋ = ⌊ 3 2 7 6 1 + 3 4 2 0 + 3 ⌋ = 1 9 0
This is what is it look like. :)