Is the information sufficient?

$\angle CAD=45^\circ$ , therefore $DF=FH$ .
$FE=\frac{FG}{2}=\frac{FH}{2}= \frac{DF}{2}$ , so the segment $DE$ is divided in thirds with $DF = \frac{2}{3}$ and $FE = EG=\frac{1}{3}$ .
This will give us ratio of $\frac{EB}{EG}=3$ .
Triangle $JBK$ is similar to triangle $BGE$ so $\frac{JK}{BK}=3$ .
But $JK=AK$ because of the $45^\circ$ angle, so $3a=2+a$ and $a=1$ . The height of triangle $ABJ=3a=3$ and the area is also $3$ .

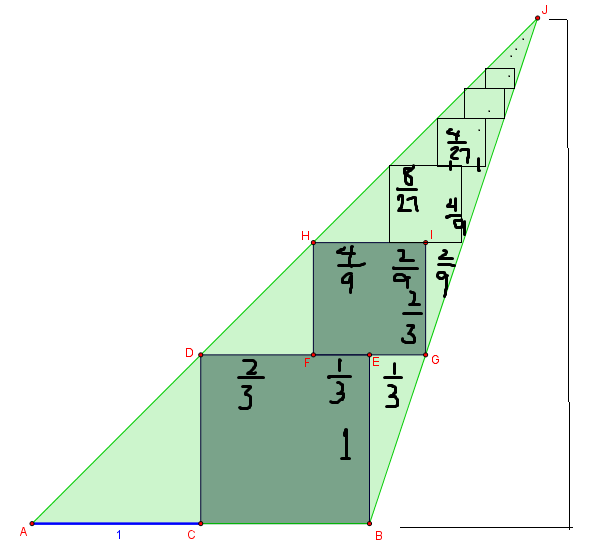
Hence, the height of the triangle is given by: $1 + \cfrac{2}{3} + \cfrac{4}{9} + ... = 3$

And therefore, the area of the triangle is: $\cfrac{3 \times 2}{2} = \boxed{3}$ .

Solution behind the height of the triangle.

Since the triangle ACD is a isosceles right triangle and DF // AC, hence, $\angle \text{DAC} = \angle \text{HDF} = 45 ^ {\circ}$ .

Let FE = x . $\implies FG = FH = FD = 2x$ .

By Whole-Part Theorem, FD + FE = BC = 1 $\implies x = \cfrac{1}{3}$ and hence, the side of square FGIH = 2x = $\cfrac{2}{3}$ .

The side of the smaller square ( i.e. $\cfrac{4}{9}$ is also obtained by doing these method. )

Now, as you observed, the sides of the square forms a infinite geometric progression, which when you add it all, it is equal to the height of the triangle.

The rest of the solution is given above. 😀😀

we can see line $FE$ satisfies two eqns: $\begin{cases} DF+FE=1\\ 2FE=DF\\ \end{cases}$ the first eqn is true since the two segments are just part of another segment with length 1, the second is true since it is similar to triangle $\delta ADC$ , meaning it is isosceles. we can solve to get $FE=\frac{1}{3}$ . we consider two similar triangles: $ABJ, DGJ$ . we can see that $\dfrac{[DGJ]}{[ABJ]} = \left(\dfrac{DG}{AB}\right)^2 = \left(\dfrac{1+\frac{1}{3}}{2}\right)^2=\dfrac{4}{9}$ the area of the trapazoid $[ABGD] = \dfrac{DC(DG+AB)}{2}=\dfrac{5}{3}$ we can see $[DGJ]+[ABGD]=[ABJ]$ let $v= [ABJ]$ . then $\dfrac{4}{9} v+\dfrac{5}{3}= v\to v= \boxed{3}$

Similar triangles and squares: $\triangle ABJ \sim \triangle DGJ;\ \ \ \ \square BCDE \sim \square GFHI;\ \ \ \ \triangle ACD \sim \triangle DFH.$

From $AC = CB$ it follows that $DF = FG$ . On the other hand, $DF + \tfrac12 FG = 1$ . From this we conclude $DF = \tfrac23,$ which is also the ratio of similarity, $x = \tfrac23$ .

We could continue to build smaller squares on top of the existing square, in the same manner. The top of this infinite tower converges to point $J$ . Thus the height of $J$ above base $AB$ is $y = 1 + x + x^2 + \cdots = \frac1{1-x} = \frac1{1-\tfrac23} = 3.$ The area of the triangle is therefore $\tfrac12\cdot AB \cdot y = \boxed{3}.$

Note that the homothety mapping $FGIH$ to $CBED$ has center at the intersection of $DH$ and $BG$ , which is just $J$ . Since $E$ is mapped to the midpoint $M$ of $CB$ with respect to this homothety, then $J, E, M$ are collinear. Let $h$ be the length of the altitude from $J$ to line $DE$ , and let $h'$ be the length of the altitude from $J$ to $AB$ . Note that $h'-h=BE=1$ . By similar triangles $\triangle JDE \sim\triangle JAM$ , it follows that $\dfrac{h}{h'} = \dfrac{DE}{AM} = \dfrac{1}{1+\frac{1}{2}} = \dfrac{2}{3}$ $\implies h' = \dfrac{3}{2}h = \dfrac{3}{2}(h'-1)=\dfrac{3}{2}h'-\dfrac{3}{2}\implies \dfrac{1}{2}h'=\dfrac{3}{2}\implies h'=3$ Thus, the area of $\triangle ABJ$ is $\dfrac{1}{2}\cdot AB\cdot h' = \dfrac{1}{2}\cdot 2\cdot 3=\boxed{3}$ done.

Note that this solution is particularly nice in that it works with the exact same calculations no matter what length $AC$ was; in particular, it does not rely on the fact that $\angle CAD=45^{\circ}$ in any way. $\Box$

Essentially, the answer is the height of the triangle. If point A is the origin then we can create two lines y=x and y=3x-6. They intersect at a point with a y value of three, so that is the answer

Triangles ACD and BCD are two equal right isosceles then triangle ABD is also right isosceles. Then $\angle CAD=45^\circ$ which means $\angle GDH$ is also $45^\circ$ (alternate angles) and $\angle HGD = 45^\circ$ then triangle DGH is right isosceles at H (since it has two $45^\circ$ angles) but [HF] is a height of it then it is a median which means $DF=FG =2FE$ therefore $DF+FE=1$ then $3FE=1$ therefore $FE = \frac{1}{3}$ then $DG=4FE= \frac{4}{3}$ . Now, $(AB) || (DG)$ then $\frac{DG}{AB}=\frac{\frac{4}{3}}{2}=\frac{2}{3}$ then $\frac{JD}{JA}= \frac{2}{3}$ then $JA=3DA$ , but $AD = \sqrt{2}$ (Pythagorean Th.) then $AJ=3\sqrt{2}$ Therefore Area of Triangle $ABJ=\frac{1}{2}BD \times AJ = \frac{\sqrt{2} \times 3\sqrt{2} }{ 2} = 3$ .

After we find that EG = 1/3 we know that EB = 1 then we can find the angle <GBE by doing Tan<GBE = $\frac{1/3}{1}$

<GBE = 18.43

therefore <JBA = 90 + 18.43

<JBA = 108.43

we know that <A = 45

we can find <J which is 180 - 45 - 108.43

<J = 26.56

now we can find the length of AJ by doing

$\frac{AJ}{sin108.43}$ = $\frac{2}{sin26.56}$

Which gets us to AJ = 4.2435

and so after we find AJ we can calculate the area by the formula $\frac{(AJ * AB * sin <A)}{2}$ $\frac{4.2435 * 2 * sin45}{2}$ which gets us to 3.000.

Suppose we construct line segments between D and B and between H and G. Since AC = CD, angle CAD is 45 degrees. So is angle CBD, since segment DB is the diagonal of a square, and bisects a 90 degree angle. Similarly, angles FDH and FGH are also 45 degrees.This means that the square constructed in triangle DGJ is the same proportion to the square inside triangle ABJ as the triangle DGJ is to triangle ABJ. This construction can therefore be continued ad infinitum. As the upper right corner of the square is always interior to the triangle, it asymptotically approaches vertex J. If we now draw a line through all these corners through the baseline, it is clear that it must bisect segment BC at point K, since E bisects FG, and the fact that all the squares are constructed similarly. The tangent of angle IEG is 2, so it must also be the tangent of angle JKB. Finally, we drop a perpendicular to an extension of the baseline, intersecting at point L. Since AL = JL, and KL = 1/2 JL, KL = 1/2 AL. AL = AC + 1/2 BC = 1.5, so AL = JL = 3. The area of triangle ABJ is 2 * 3 / 2 = 3.

Very simple:

AB = 2, DG = 4/3, vertical distance between AB and DG = 1. Assume vertical distance between DG and Jamal = x.
DG/AB = x / (x + 1)
x/(x+1) = 4/3/2 = 2/3
3x = 2x + 2
Solving for x, x = 2

height = 3

Area = 1/2 × 2 × 3 = 3