Is the question correct ?
A B C D is a trapezium with A B ∣ ∣ C D . B K = 5 and B C = 1 2 , A F = F D and ∠ C F K = 9 0 ∘ as shown in the figure. Find the area of the trapezium A B C D .
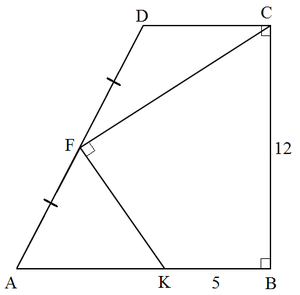
The answer is 108.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Chew, nice solution, mine was much longer.
I think my solution is a little better than all other solutions posted here, so if you like please write it up (in a better way) as a solution too sir.
So I simply extended CF to cut AB (according to your figure) at E. And now by congurency of CFD and AFE yields KE=KC=13 which makes E B=18 implying area of triangle CEB=area of trapezium= 2 1 2 × 1 8 = 1 0 8
Not much difference but your solution involves a little extra hard work...
Use the Midline of the trapezium and triangle to calculate FG FG= AB+CD/2
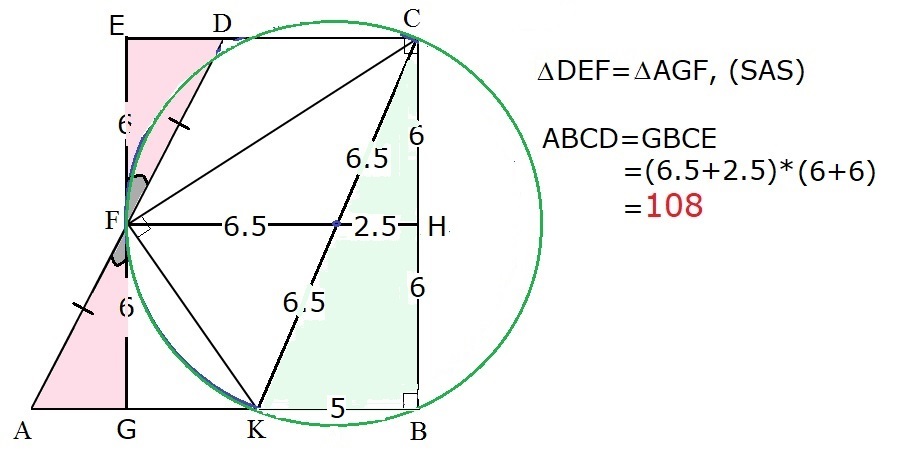
R i g h t Δ C K B i s 5 − 1 2 − 1 3 , C K = 1 3 .
How do we know that FH - 2.5 = 6.5?
Log in to reply
Theorem : Diameter of a circle subtends right angle at the circle. Reversing this theorem, we get that CK is diameter. So, OK = OF = OC.
Note : O is center of the circle. And OK, OF, and OC are radii.
Let the intersection of CK and FH be O. Observe that FH is the perpendicular bisector of CB and hence CK, so O is the midpoint of CK, so OF = 6.5.
Similar triangles CKB and COH with ratio 2:1. Hence 2:1 = KB:OH, so OH = 2.5.
As an aside, the circle in the figure should also pass through B.
It need not pass through D (in part because AFD can be any line).
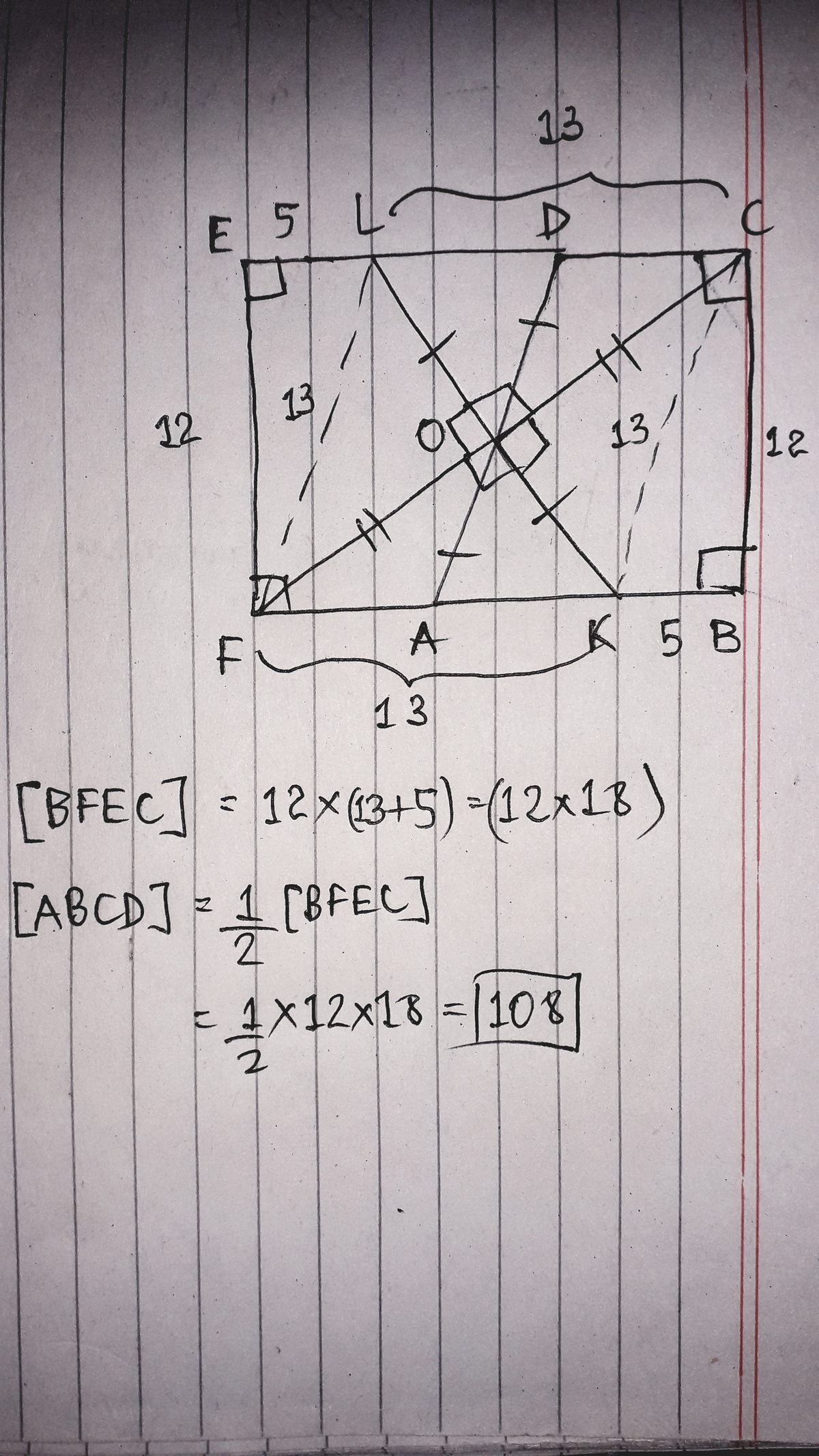
A d d an inverted copy of trapezium ABCD to the side AD..
T h i s makes F L C K a r h o m b u s . M a k i n g F L = L C = C K = K F = 1 3
Draw C K and rotate △ C D F 1 8 0 ° about F :
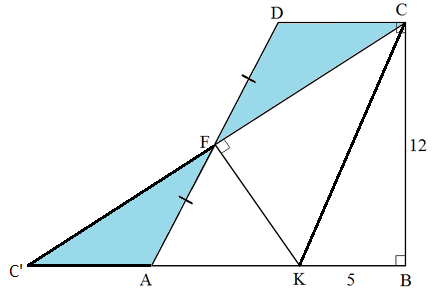
By Pythagorean's Theorem on △ B C K , K C = 1 3 .
Since F C ′ ≅ F C , ∠ K F C ′ ≅ ∠ K F C , and F K ≅ F K , △ K F C ′ ≅ △ K F C by SAS congruence.
Therefore K C ′ = K C = 1 3 , and the area of trapezium A B C D is A A B C D = A △ C B C ′ = 2 1 ( 1 3 + 5 ) 1 2 = 1 0 8 .
I used coordinate geometry to solve this problem. Let B = ( 0 , 0 ) , then K = ( − 5 , 0 ) and C = ( 0 , 1 2 ) , while point F = ( x , 6 ) , where x is negative.. Now, since ∠ C F K is a right angle then the dot product C F ⋅ F K = 0 . Now, C F = F − C = ( x , − 6 ) and F K = K − F = ( − 5 − x , − 6 ) , and therefore C F ⋅ F K = x ( − 5 − x ) + 3 6 = 0 ⇒ x 2 + 5 x − 3 6 = 0 ⇒ ( x + 9 ) ( x − 4 ) = 0 ⇒ x = − 9 , because x < 0 . The area of the trapezium a = 2 1 ( D C + A B ) C B = 1 2 ( − x ) = 1 2 ( 9 ) = 1 0 8 .
Let F G = x be parallel to A B and C D . and F H is perpendicular to A B . Then C G = B G = 6 , △ C F G and △ F H K are similar, and that
x 6 x 2 − 5 x − 3 6 ( x + 4 ) ( x − 9 ) ⟹ x = 6 x − 5 = 0 = 0 = 9 Since x > 0
We note that △ A F H and △ D F L are congruent, making the area of trapezium A B C D equal to the area of rectangle B C L H which is 9 × 1 2 = 1 0 8 .