Is the rope the shortest path ?
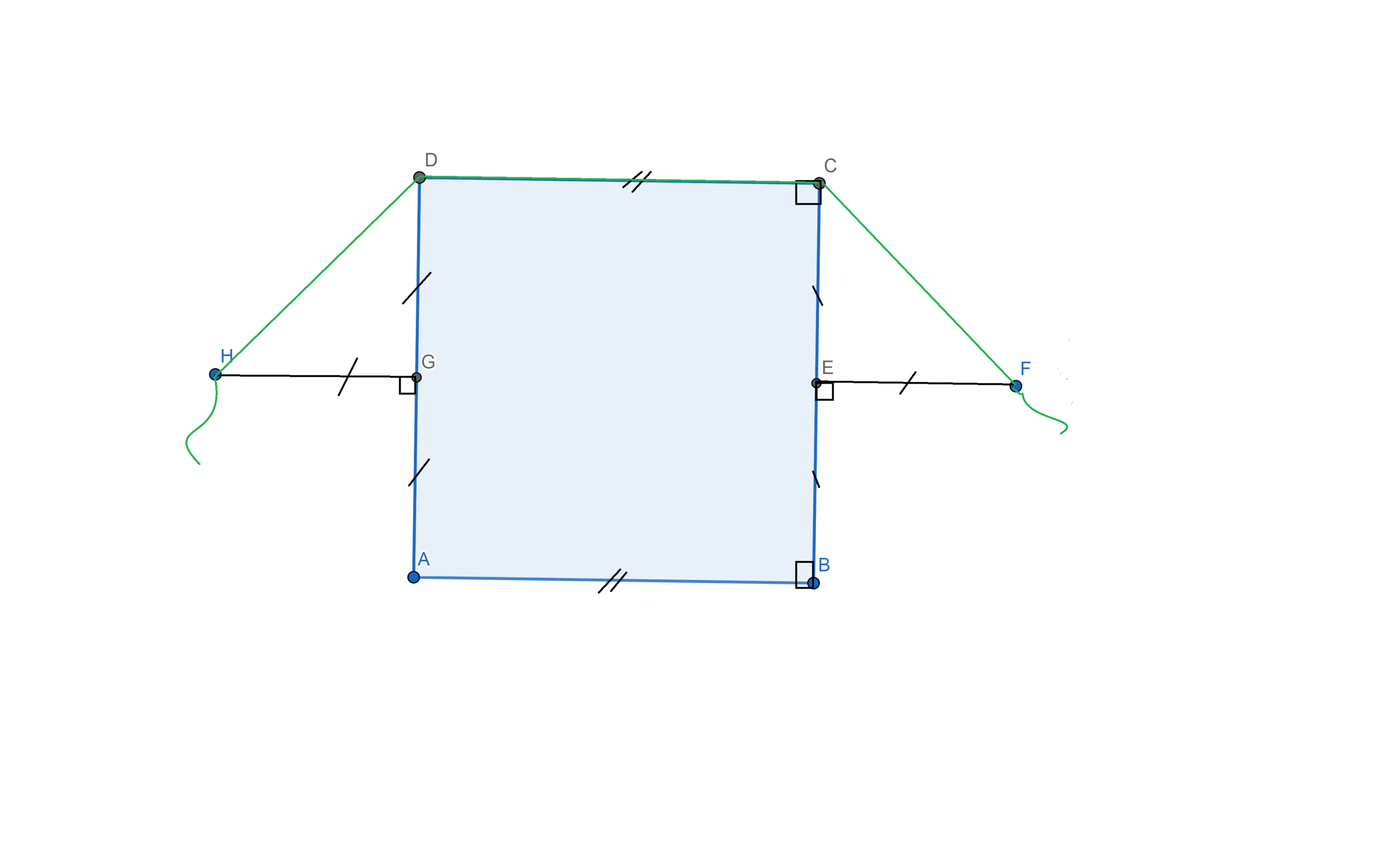
The green curve draws the shortest path between F and H that doesn't pass through the square. If the square was solid, then that curve would look like some rope that is connecting F and H and is being pulled by the two points with equal strength from both sides.
If you change the square with any other shape (that allows a shortest path), is it always true that the shortest path between F an H would look like a rope pulled by the two points ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!