Is there a centroid?
On the regular grid nine different grid points were randomly chosen. Is it true, that there always exist three chosen points, such that the centroid of the triangle or segment defined by them is a grid point?
Note: A centroid of a segment is the midpoint of the segment.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For each of the nine points we order them coordinates' remainder m o d 3 . There are nine possibilities: ( 0 ; 0 ) , ( 0 ; 1 ) , ( 0 ; 2 ) , ( 1 ; 1 ) , … , ( 2 ; 2 )
There are two cases:
C a s e 1 : From the nine possibilities maximum 4 appears between the nine points.
Then there will be three points, the coordiantes of which make the same remainders ( Pigeonhole Principle ), so their coordiantes are: ( 3 m + r ; 3 M + q ) , ( 3 n + r ; 3 R + q ) , ( 3 k + r ; 3 K + q )
The centroid of this triangle (defined by this three points) will be a grid point, because C = ( 3 3 m + r + 3 n + r + 3 k + r ; 3 3 M + q + 3 N + q + 3 K + q ) = ( m + n + r + k + r ; M + N + K + q )
C a s e 2 : From the nine possibilites minimum 5 appears between the nine points.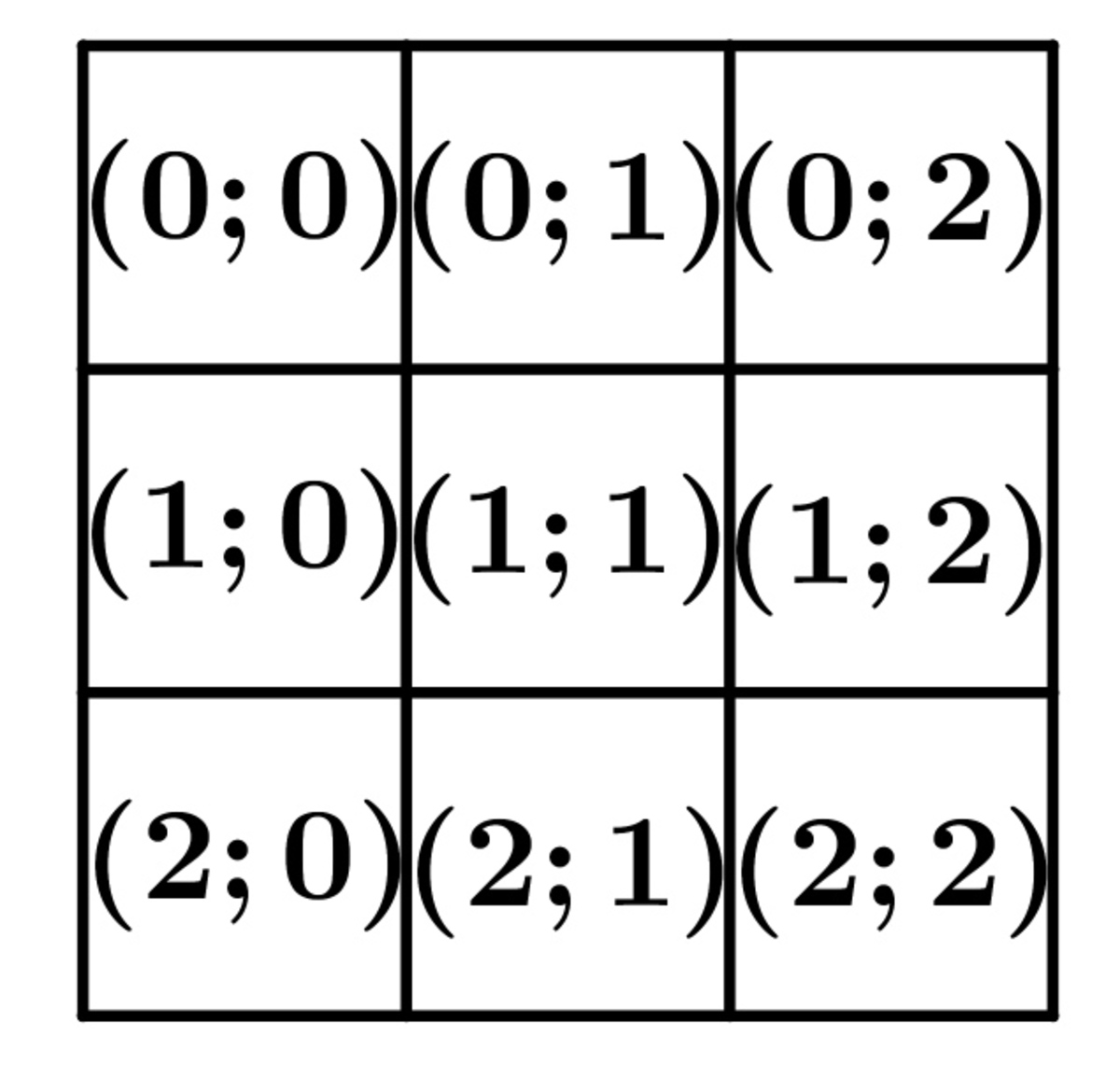
Then it is easy to see that if we choose 5 cells from the square above, there will be three, which are in the same row or column or the three cells are in different rows and different columns. These three points define a triangle which centroid is a grid point.