Is there an elegant method?

First, let's observe that point P lies on a line given.

Now let's consider a parabola $y=x^2$ and a line $y=mx+c$ intersecting it in points $A(a,a^2)$ and $B(b,b^2)$ . Line $AB$ intersects Y-axis at point $P$ . Point $B$ is reflected about point $P$ giving point $B1$ .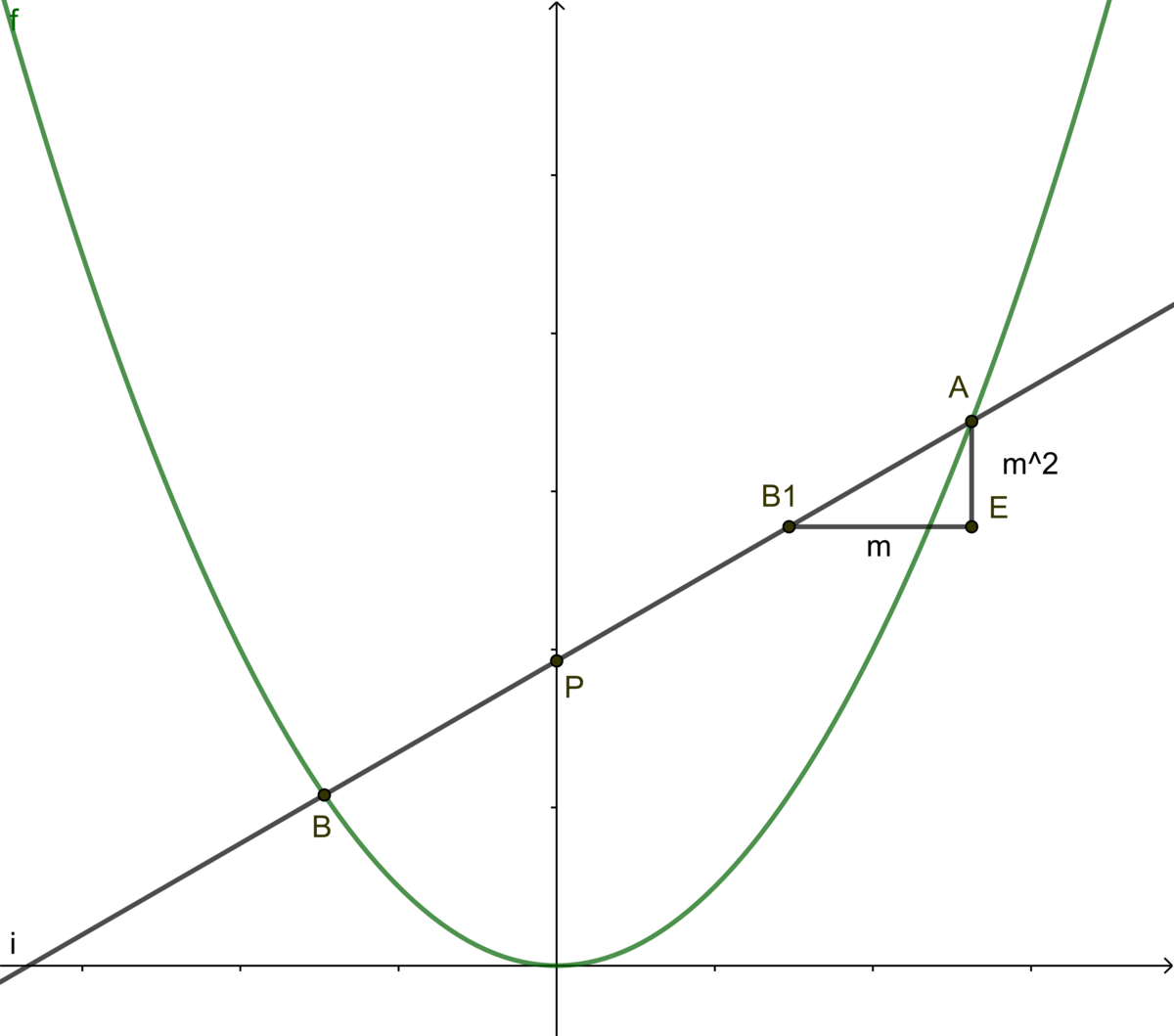

We have the following:

$m=\dfrac{a^2-b^2}{a-b}=a+b=B1 E$

$m=\dfrac{AE}{B1 E} \Rightarrow AE=m^2 \Rightarrow AB1=AP-BP=m \sqrt{m^2+1}$

This means that this difference in lengths is constant for a given slope, regardless of the value of $c$ .

In the specific scenario given our parabola is rotated by 90 degrees, which gives $m=\dfrac{1}{\sqrt{3}}$ . This gives $PA-PB=m \sqrt{m^2+1}=\boxed{\dfrac{2}{3}}$