Is there a sequence here? (no)
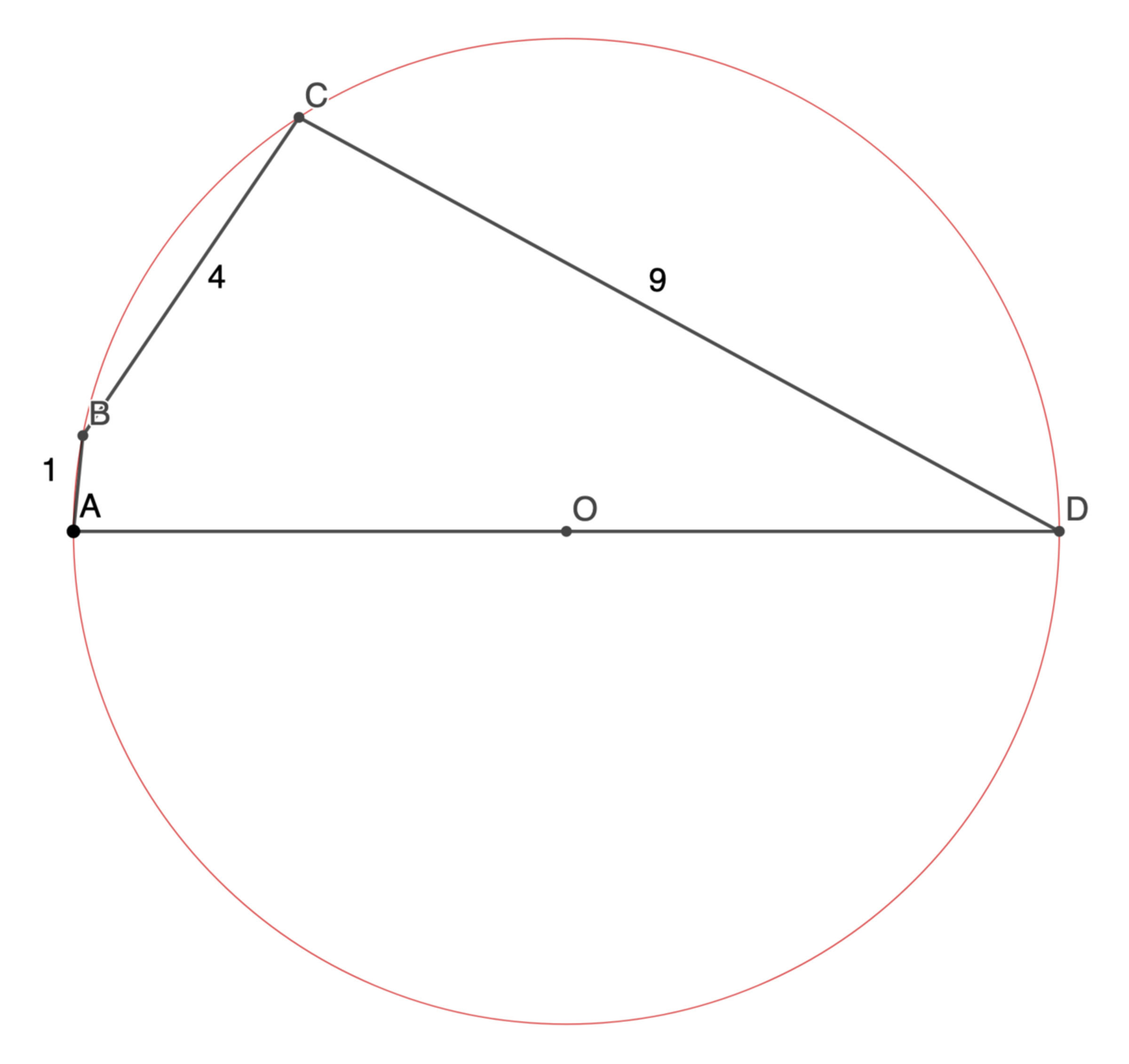
A B C D is a cyclic quadrilateral where A B = 1 , B C = 4 , C D = 9 . O is the circumcenter. A O D is a diameter. What is A D ? Submit ⌊ A D ⋅ 1 0 4 ⌋
The answer is 102482.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Method 1
Let A D = x and draw B D . By Thales's Theorem , ∠ A B D = 9 0 ° , so that B D = x 2 − 1 , sin A = x x 2 − 1 , and tan A = x 2 − 1 .
As a cyclic quadrilateral , opposite angles are supplementary, so sin A = sin D .
The area of the quadrilateral is then A A B C D = A △ A B D + A △ B C D = 2 1 x sin A + 2 1 3 6 sin D = 2 x 1 ( x + 3 6 ) x 2 − 1 .
The area of the quadrilateral is also given by A A B C D = 4 1 ( a 2 − b 2 − c 2 + d 2 ) tan A = 4 1 ( 1 2 − 4 2 − 9 2 + x 2 ) x 2 − 1 = 4 1 ( x 2 − 9 6 ) x 2 − 1 .
Therefore, A A B C D = 2 x 1 ( x + 3 6 ) x 2 − 1 = 4 1 ( x 2 − 9 6 ) x 2 − 1 , which rearranges to x 3 − 9 8 x − 7 2 = 0 and solves to x ≈ 1 0 . 2 4 8 2 for x > 0 and x = 1 .
Therefore, ⌊ A D ⋅ 1 0 4 ⌋ = 1 0 2 4 8 2 .
Method 2
Let a = A B = 1 , b = B C = 4 , c = C D = 9 , and d = A B = x .
By Parameshvara's Theorem , R = 4 1 ( s − a ) ( s − b ) ( s − c ) ( s − d ) ( a b + c d ) ( a c + b d ) ( a d + b c ) , or 2 x = 4 1 1 6 1 ( − x + 1 4 ) ( x + 1 2 ) ( x + 6 ) ( x − 4 ) ( 4 + 9 x ) ( 9 + 4 x ) ( x + 3 6 ) .
This expands to x 6 − 1 9 6 x 4 − 1 4 4 x 3 + 9 6 0 4 x 2 + 1 4 1 1 2 x + 5 1 8 4 = 0 .
Taking the square root of both sides gives x 3 − 9 8 x − 7 2 = 0 which solves to x ≈ 1 0 . 2 4 8 2 for x > 0 .
Therefore, ⌊ A D ⋅ 1 0 4 ⌋ = 1 0 2 4 8 2 .
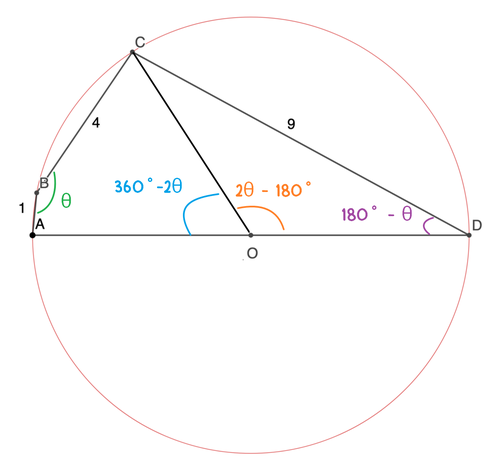
Let θ denote the measure of the angle ∠ A B C .
Since
A
B
C
D
is a cyclic quadrilateral, we have
∠
A
D
C
=
1
8
0
∘
−
θ
.
∠
A
O
C
=
2
×
∠
A
C
D
=
3
6
0
∘
−
2
θ
.
Thus,
∠
C
O
D
=
1
8
0
∘
−
∠
A
O
C
=
2
θ
−
1
8
0
∘
>
0
.
And so,
9
0
∘
<
θ
<
1
8
0
∘
.
And let r denote the radius of the circle. We want to find the diameter A D = 2 r .
Apply cosine rule on △ C O D , 2 r 2 − 2 r 2 cos ( 2 θ − 1 8 0 ∘ ) = 9 2 ⇔ 2 r 2 ( = 2 cos 2 θ 1 + cos ( 2 θ ) ) = 8 1 ⇔ r cos θ = − 2 9 ( ∵ cos θ < 0 )
Similarly, apply cosine rule on △ A B C , ( A C ) 2 = 1 2 + 4 2 − 2 ⋅ 1 ⋅ 4 cos θ = 1 7 − 8 cos θ
Likewise, apply cosine rule on △ A O C , ( A C ) 2 = 2 r 2 ( = 1 − cos ( 2 θ ) = 2 sin 2 θ 1 − cos ( 3 6 0 ∘ − 2 θ ) ) = 4 r 2 sin 2 θ = 4 r 2 − 4 r 2 cos 2 θ = 4 r 2 − 4 ( − 2 9 ) 2 = 4 r 2 − 8 1
Comparing the last two equations above, 1 7 − 8 cos θ 1 7 r − 8 r cos θ 1 7 r − 8 ( − 2 9 ) 2 r 3 − 4 9 r − 1 8 = = = = 4 r 2 − 8 1 4 r 3 − 8 1 r 4 r 3 − 8 1 r 0
Thus, r ≈ 5 . 1 2 1 4 1 . The answer is ⌊ A D ⋅ 1 0 4 ⌋ = 1 0 2 4 8 2 .
nice approach!
B D = A D 2 − A B 2 ⇒ B D = x 2 − 1 and
A C = A D 2 − C D 2 ⇒ A C = x 2 − 8 1
By Ptolemy’s theorem on cyclic quadrilateral A B C D , A C ⋅ B D = A B ⋅ C D + B C ⋅ A D ⇔ x 2 − 8 1 ⋅ x 2 − 1 = 1 × 9 + 4 x ⇔ ( x 2 − 8 1 ) ( x 2 − 1 ) = ( 9 + 4 x ) 2 ⇔ x 4 − 9 8 x 2 − 7 2 x = 0 ⇔ x > 0 x 3 − 9 8 x − 7 2 = 0 This cubic has one positive solution, x ≈ 1 0 . 2 4 8 2 0 0 9 8 0 6 4 7 4 .
For the answer, ⌊ A D ⋅ 1 0 4 ⌋ = 1 0 2 4 8 2 .