Is there an alternative?
There are 12 different chocolates placed on a table along a straight line. In how many ways can a person choose 4 of them such that no 2 of the chosen chocolates lie next to each other?
The answer is 126.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Excllent work @Archit Agrawal .
i too did the same!! . number of ways of selecting is the same as number of ways of placing
Great solution!!
Ah, this is a nice interpretation! I didn't know stars and bars was hidden in plain sight!
Let S be the set of 4 -tuples ( a , b , c , d ) of integers where 1 ≤ a < b < c < d ≤ 9 , and let T be the set of 4 -tuples ( p , q , r , s ) where 1 ≤ p , q , r , s ≤ 1 2 and q − p , r − q , s − r ≥ 2 . Then f : S → T is a bijection, where f ( a , b , c , d ) = ( a , b + 1 , c + 2 , d + 3 ) ( a , b , c , d ) ∈ S Thus S and T have the same number of elements, and ∣ S ∣ = ( 4 9 ) . Thus the number of ways of choosing the chocolates is ∣ T ∣ = 1 2 6 .
This is not a solution, sorry. It's a song for starwar clone , my friend...
Here is my solution (countig) : ( 2 1 + 1 5 + 1 0 + 6 + 3 + 1 ) + ( 1 5 + 1 0 + 6 + 3 + 1 ) + ( 1 0 + 6 + 3 + 1 ) + ( 6 + 3 + 1 ) + ( 3 + 1 ) + 1 = = 5 6 + 3 5 + 2 0 + 1 0 + 4 + 1 = 1 2 6 P.S.- Can you understand it?
thanks for the song friend and welcome back....
Log in to reply
Do you like Radiohead, what about this? . Your profile photo is very similar to... Look at the left bottom corner...
Log in to reply
Yeah I've heard them....mine profile photo has fozzy .
This is equivalent to asking how many ways can you arrange 4 red chocolates and 8 blue chocolates so that none of the red chocolates are next to each other.
Remove 3 blue chocolates from consideration, and store them for later.
Then there are 9C4 ways to arrange the remaining red and blue chocolates.
Add the remaining 3 chocolates so that they are between the four chocolates you selected. Now the four chocolates you selected are guaranteed to be separated by at least one chocolate.
Thus there are exactly 9C4 ways!
I counted opposite those where two or more are consecutive and get 369 And substract from 12C4=495, number of ways to choose any 4. So answer is 495-369=126
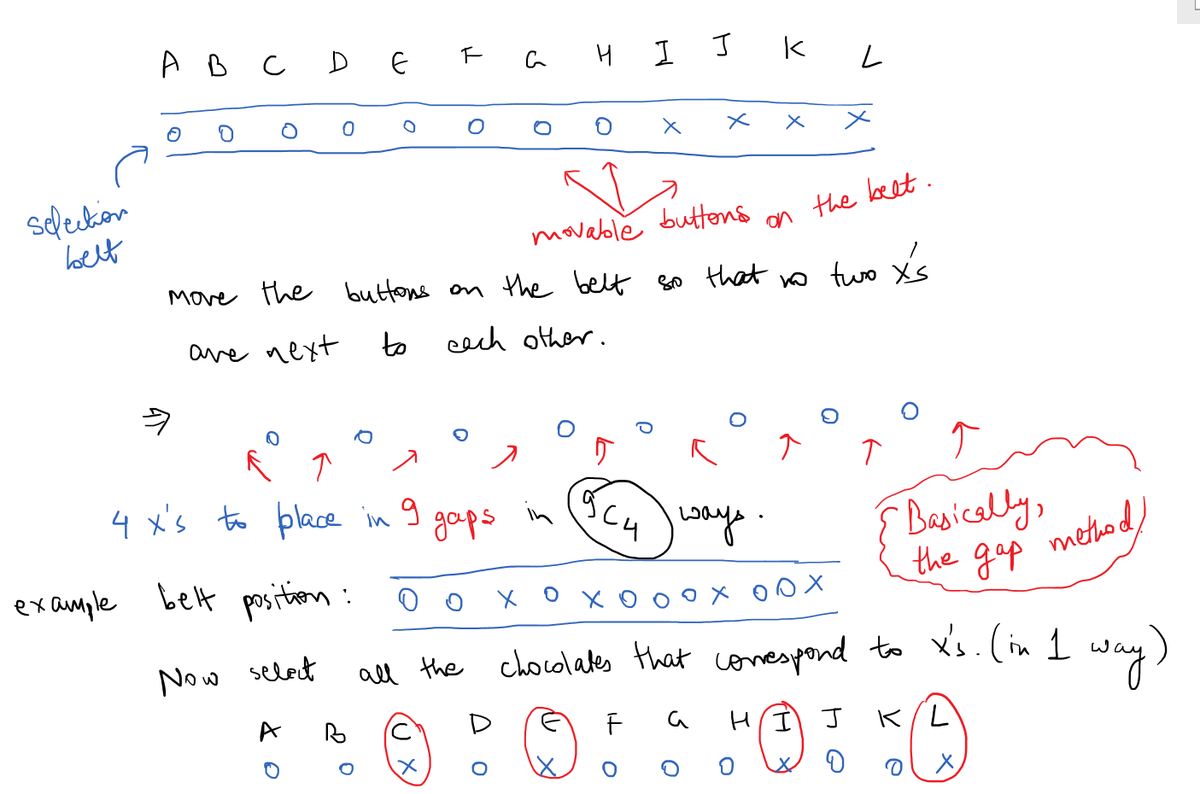
Follow up question: What if instead of a straight line, they were sitting around a circle?
@Ashish Gupta ..nice use of gap method and to answer to your follow up question , I have posted a modified version of your problem ..try this ... I will provide a solution later if no one adds a solution .
We can solve it by gap method i.e. place 8 chocolates in a row then there will be 9 gaps then we select 4 gaps from these which will be the answer 9C4=126.