Is There An Easy Way To Solve This?
− = 1 2 3 4 5 6 7 8 9 × 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 8 × 1 2 3 4 5 6 7 9 0 ?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
45 solutions
Cool I just used smaller numbers instead
amazing... i did it the same way ;)
I didn't get it clearly
Log in to reply
He is saying that to solve this you simply have to put 1 2 3 4 5 6 7 8 9 = x Meaning that you simply replace 1 2 3 4 5 6 7 8 9 by x because you know that 1 2 3 4 5 6 7 8 9 = x .Look 1 2 3 4 5 6 7 8 8 = 1 2 3 4 5 6 7 8 9 − 1 = x − 1 and 1 2 3 4 5 6 7 8 9 0 = 1 2 3 4 5 6 7 8 9 + 1 = x + 1 so you replace all these values into the equation and solve.
A=( 9n+2014)^2- 100n^2
perfect!!!!!!!!!!! I also did in this way!
I exactly did in this way
well-done ,
I did something like this, but not equaled the equation to give y,
I did something like this, but not equaled the equation to give y.
Hey! I did it the same way
best way to do it
((x +1) (x -1)) = ( x -1) ?????????
Amazing.....
( 1 2 3 4 5 6 7 8 9 × 1 2 3 4 5 6 7 8 9 ) − ( 1 2 3 4 5 6 7 8 8 × 1 2 3 4 5 6 7 9 0 ) = 1 2 3 4 5 6 7 8 9 2 − ( 1 2 3 4 5 6 7 8 9 2 − 1 2 ) 1 2 3 4 5 6 7 8 9 2 − 1 2 3 4 5 6 7 8 9 2 + 1 2 = 1
That's interesting.
Let's make this logic:
1 2 3 4 5 6 7 8 9 = x
Subtitude:
x × x = x 2
( x − 1 ) × ( x + 1 ) = x 2 − ( 1 ) 2
So determine both of them:
x 2 − ( x 2 − ( 1 ) 2 ) = x 2 − x 2 + 1 = 1
Let x = 1 2 3 4 5 6 7 8 9
So, ( 1 2 3 4 5 6 7 8 9 × 1 2 3 4 5 6 7 8 9 ) − ( 1 2 3 4 5 6 7 8 8 × 1 2 3 4 5 6 7 9 0 )
becomes x 2 − ( x − 1 ) ( x + 1 )
Upon solving, we get -
= x 2 − [ x 2 − 1 2 ]
= x 2 − x 2 + 1
= 1
Used Algebraic Identities:
x × x = x 2
x 2 − y 2 = ( x − y ) ( x + y )
that's me!
(89 * 89)-(88 * 90) or, (9 * 9)-(8 * 10)
or 1 * 1-0 * 2
its just a simple fact ,of basic algebra
You know there is just a more easy way to answer it. More easy than you think. Just look to the last number to each set of numbers. The last numbers are 9, 9, 8 and 0. Automatically the zero there means 10 because the 8 and ten makes the 9 in between which makes 0 not appropriate. This is (9 x 9) - (8 x 10) = ? Then, 81 - 80 = 1. Easy eh? Its just Common Sense. That's all. If u encounter problems like this, why wont you follow my technique... it may come in handy.
starting with small number 24 24=576 and 25 25= 625 so differance is 49(24+25) so here also we can calculate like this only 123456789 123456789= 123456788 123456788+123456788+123456789 equation (1) and 123456788 123456790= 123456788 (123456788+2) =123456788*123456788+123456788+123456788 equation (2) subtracting equ 1 and 2 we will get answer as 1
Not so getting it as well
this is a more complicated method
1 2 3 4 5 6 7 8 9 2 − ( 1 2 3 4 5 6 7 9 0 × 1 2 3 4 5 6 7 8 8 ) = 1 2 3 4 5 6 7 8 9 2 − ( 1 2 3 4 5 6 7 8 9 2 − 1 ) = 1 2 3 4 5 6 7 8 9 0 2 − 1 2 3 4 5 6 7 8 9 2 + 1 = 1
Cool problem. I chose to write a Java program to solve, since I didn't see it could be more easily solved by using a variable instead of 123456789. I had to learn the BigInteger Class, but here's what I got.
import java.math.BigInteger;
public class BrilliantQuestion{
public static void main(String[] args) {
BigInteger b1 = new BigInteger("123456789");
BigInteger square = b1.pow(2);
BigInteger b2 = new BigInteger("123456788");
BigInteger b3 = new BigInteger("123456790");
BigInteger product = b2.multiply(b3);
BigInteger difference = square.subtract(product);
System.out.println("123456789^2 - (123456788 * 123456790) is " + difference);
}
}
Any n: n^{2} - (n - 1)(n + 1) = n^{2} - (n^{2} - 1) = 1. Simple as pie.
subtract 123456788 from each number so it will be :
1 * 1-0 * 2=1-0=1
For every three consecutive numbers, the square of the middle term minus the product of extreme terms is always 1.
let 123456789 = x , 123456788=123456789-1 and 123456790=123456789+1 then the problem will be : (x*x) - [(x-1) (x+1)] = x^2 - [x^2 - 1^2] = - [- 1^2] = 1
#
logical question..... if 123456789 = x , x(x) = x^2, (x-1) (x+1), = x^2 - (1)^2, so, x^2[x^2 -(1)^2], =x^2-x^2+1, =1
Since a^2 - (a-1)(a+1)=1...yeah
Consider a=123456789 => thereby the given problem would become a^2 - [(a-1)(a+1)] => a^2 - [a^2 - 1] => a^2 - a^2 +1 both a^2 (a squared) get cancelled and remains "1"
Use x for 123456789: x^2-((x-1)(x+1))=y result: y = 1
Let 123456789=x then x2-[(x-1)(x+1)}= x2-(x2-1)=x2-x2+1=1
Notice that the numbers are 123456788, 123456789, and 123456790. Since 123456789 is the middle value, we let it become N. N-1 = 123456788 N+1 = 123456790 now we simplify the mathematical sentence: =(N*N) - ( N-1) * (N+1) recall that ( N-1) * (N+1) = N^2 - 1; =N^2 - (N^2 - 1) =N^2 - N^2 + 1 =1
(x^2) - (x+1)(x-1) =x^2-(x^2-1) =x^2-x^2+1 =1
just replace '123456789' by 'x'.... the problem will look much simpler than it is.....
Let 1234567890 be a
=>(a-1)^2-((a-2) x a) = a^2+1-2a-a^2+2a=1
I didn't get it first but I got
take 123456789=a; then (a^2)-(a-1*a+1)=1
(a^2) (a-1) (a+1)=(a^2)-(a^2)+1=1
(123456789)^2 - (123456788 x 123456790) = (123456789)^2 - [(123456789 - 1) x (123456789 +1)] = (123456789)^2 - [(123456789)^2 - 1^2)] = - (-1^2) = 1
let 123456789=x
(123456789 123456789)-((123456789-1) (123456789+1))
=(x x)-((x-1) (x+1))
=x^2-(x^2-1)
=1
At first let's make 123456789 equal to x or just simply let substitute it as x, We can get on the equation that the minuend is equal to (x) times (x). Then, To get the value of the subtrahend we must observe the characteristic of the given terms. The given term is considered as the sum and difference of two squares, That 123456788 = 123456789 - 1 and 123456790 = 123456789 + 1 , and as the equation says. The subtrahend is the product of the sum and difference of those squares. Way back from our first step, We say that 123456789 is equal to (x), Then let us substitute the x into the given term, So we will get (X) (X) - (X -1)(X+1) = ? , Evaluate the equation. We will get X^2 - (X^2 - 1) ------> X^2 - X^2 + 1 = ? ------- > Then we will get 1
Do 123456789 = A, we can say A x A - (A - 1) x ( A + 1).
Let's look A x A:
A x A = A x (A -1 + 1) = A x (A - 1) + A
Looking now A x (A - 1):
A x (A - 1) = (A + 1 - 1) x (A - 1) = (A + 1) x (A - 1) - (A - 1).
So:
A x A = (A + 1) x (A - 1) - (A - 1) +A = (A - 1) x (A + 1) - A +A + 1
Puting all togheter
(A - 1) x (A + 1) - A +A + 1 - (A - 1) x ( A + 1) = 1 !!!
(123456789)^2-(123456789-1)(123456789+1) =(123456789)^2-{123456789^2-1}=1
If 123456789=a
123456789 * 123456789-123456788 * 123456790
=a * a-(a-1) * (a+1)
=a^2-(a^2-1)
=1
Let, x=123456789 so, 123456788=x-1 and 123456790=x+1 then the given problem becomes like following: x^2-{(x-1)(x+1)} =(x^2) - (x^2)+1 =1
Choose a=123456789 then a-1=123456788and a+1=123456790 then this problem gives, a^2-((a-1)(a+1))=1
Assume x=123456789 the equation becomes : x^2-((x-1)*(x+1)) x^2-(x^2-1) =1
(123456789 123456789)-(123456788 123456790) ={123456789 (123456790-1)}-{(123456789-1) 123456790} =(123456789 123456790)-123456789-(123456789 123456790)+123456790 =123456790-123456789 =1
(123456789)^2 - ((123456789-1)(123456789+1))
(123456789)^2 - (123456789)^2 +1
let 123456789 = X and calculate the rest.
let 123456789=a; so the equation becomes a^2-{(a-1)(a+1)} on solving we get the answer =1
Substitute 123456789=m
(123456789 \times 123456789)-((123456789-1) \times (123456789+1))=n
(m \times m)-((m-1) \times (m+1))=n
m^{2}-(m^{2}-1)=n
m^{2}-m^{2}+1=n
n=1
123456789^2-{(123456789-1) (123456789+1)} =123456789^2-(123456789^2-1^2) =123456789^2-123456789^2+1^2 =1^2 =1
Just focus on the last two digits. (89^2)-(88*90)=1
(123456789)^2 - (123456788 x 123456790) = (123456789)^2 - {(123456789 -1) x (123456789 + 1)} = (123456789)^2 - {(123456789)^2 - 1} = (123456789)^2 - (123456789)^2 + 1 = 1
So:
( 1 2 3 4 5 6 7 8 9 × 1 2 3 4 5 6 7 8 9 ) − ( 1 2 3 4 5 6 7 8 8 × 1 2 3 4 5 6 7 9 0 )
We can put it in the form:
1 2 3 4 5 6 7 8 9 2 − ( ( 1 2 3 4 5 6 7 8 9 − 1 ) ( 1 2 3 4 5 6 7 8 9 + 1 ) ) =
1 2 3 4 5 6 7 8 9 2 − ( 1 2 3 4 5 6 7 8 9 2 + 1 2 3 4 5 6 7 8 9 − 1 2 3 4 5 6 7 8 9 − 1 ) =
Then:
1 2 3 4 5 6 7 8 9 2 − 1 2 3 4 5 6 7 8 9 2 + 1 = 1
Right the answer is 1 because n^2 - (n-1)(n+1) = 1 for all n.
Proof:
: n^2 - (n-1)(n+1)
= n^2 - (n^2 - 1)
= 1
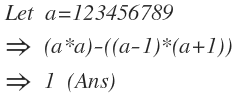
Substituting 1 2 3 4 5 6 7 8 9 by x :
( 1 2 3 4 5 6 7 8 9 × 1 2 3 4 5 6 7 8 9 ) − ( 1 2 3 4 5 6 7 8 8 × 1 2 3 4 5 6 7 9 0 )
( x 2 ) − ( ( x − 1 ) ( x + 1 ) ) = y
x 2 − ( x 2 − 1 ) = y
x 2 − x 2 + 1 = y
y = 1
So ( 1 2 3 4 5 6 7 8 9 × 1 2 3 4 5 6 7 8 9 ) − ( 1 2 3 4 5 6 7 8 8 × 1 2 3 4 5 6 7 9 0 ) = 1
In general form ( x 2 ) − ( ( x − n ) ( x + n ) ) = n 2