Is there even a formula? 🤔
Billy and Tom are playing the following game:
On his first turn Billy writes down the numbers 2, 1 and 2 as shown.
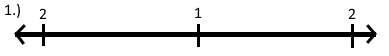
Tom afterwards writes down the sum of every two consecutively positioned numbers in-between them. Therefore the sheet of paper starts to look a bit like this:
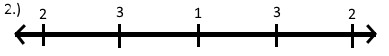
In imitation of Tom's actions, Billy writes down the next batch of sums in the same way:
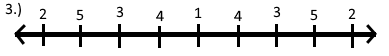
The game finishes when there will be no more numbers 100 written. Help Billy and Tom figure out how many 100's they will have placed since they are too lazy to count them.
Bonus: Try to find a formula for every number .
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's just look at the left half of the line. So there's a 2 on the left and a 1 on the right. Every value written down in between is going to be an integer linear combination of these boundary values. Let's call them α and β instead of 2 and 1 for now.
The first value we write down is α + β . The next two are 2 α + β and α + 2 β . The next four are 3 α + β , 3 α + 2 β , 2 α + 3 β , α + 3 β . And so on. If we represent m α + n β as [ m n ] , then successive steps yield [ 1 1 ] , [ 2 1 ] , [ 1 2 ] , [ 3 1 ] , [ 3 2 ] , [ 2 3 ] , [ 1 3 ] . This is exactly how the terms of the Farey sequence are generated. From two adjacent fractions n 1 m 1 , n 2 m 2 , we generate n 1 + n 2 m 1 + m 2 . It is well-known that iterating this process will generate every fraction in lowest terms exactly once.
Hence the number of 1 0 0 s will be the number of ways to write m α + n β = 1 0 0 where m , n are relatively prime. Let's substitute back now: 2 m + n = 1 0 0 . Now the general answer will follow from a lemma:
Lemma: If N ≥ 3 , the number of solutions in nonnegative coprime integers m , n to the equation 2 m + n = N is ϕ ( N ) / 2 .
Proof: There must be a fancy way to do this, but I don't see it. Take cases. If N is odd, then every positive integer m < N / 2 that is coprime to N will produce one solution. There are ϕ ( N ) / 2 of these. If N is even, then n = 2 k and we get m + k = N / 2 with m odd. Then if N / 2 is odd, then k is even and we are in the previous case, so there are ϕ ( N / 2 ) / 2 solutions, which equals ϕ ( N ) / 2 . If N / 2 is even, then every positive integer m ≤ N that is coprime to N / 2 will produce a solution, so the answer is ϕ ( N / 2 ) = ϕ ( N ) / 2 .
At any rate, the lemma shows that the number of N s on the left half of the line is ϕ ( N ) / 2 , so the total number of N s is twice that, or ϕ ( N ) . For N = 1 0 0 this gives 4 0 .