Is this defined?

A= $\dfrac{1}{p}$ , where p=x+10+ $\dfrac{25}{x}$ .

Minimum value of x+ $\dfrac{25}{x}$ is 10 (A.M.-G.M. inequality). So the minimum value of p is 20. Therefore the maximum value of A is $\dfrac{1}{20}$ when x=5

This problem is in the realm of calculus.

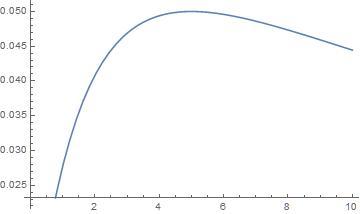
The maximum occurs at a value of $x$ where the value of first derivative of the function $x\to\frac{x}{(x+5)^2}$ is $0$ .

$\frac{\partial \frac{x}{(x+5)^2}}{\partial x}\Rightarrow \frac{1}{(x+5)^2}-\frac{2 x}{(x+5)^3}$

$\frac{1}{(x+5)^2}-\frac{2 x}{(x+5)^3} \Rightarrow (x+5)-2 x=0 \Rightarrow x=5$

$\frac{\partial ^2\frac{x}{(x+5)^2}}{\partial x\, \partial x} \Rightarrow \frac{6 x}{(x+5)^4}-\frac{4}{(x+5)^3}$ evaluated at $x=5$ is $-\frac{1}{1000}$ , of which the important fact is that the value is negative and therefore the extrema is a maximum. If it were positive, then it would be a minimum. If zero, then is would be a "saddle", a level spot in the function.

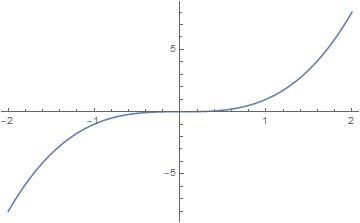
To illustration the last point, $x\to x^3$ :

$\frac{\partial x^3}{\partial x} \Rightarrow 3x^2$ . That equation has a double root at $x=0$ . $\frac{\partial ^2x^3}{\partial x\, \partial x} \Rightarrow 6x$ evaluated at $x=0$ is also $0$ . This indicates a level spot.