Is this enough?
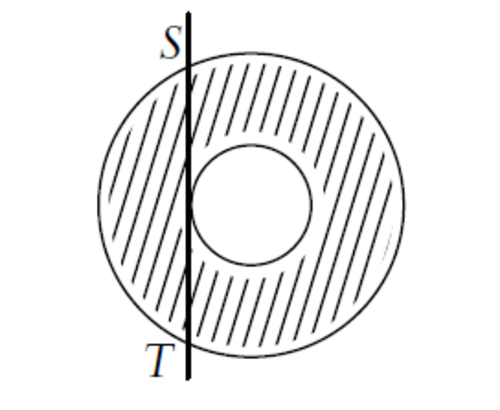 In the above diagram, the line ST is tangent to the smaller of two concentric circles, and is 36 cm long. The area of the annulus (shaded region) can be written as
a
π
.
In the above diagram, the line ST is tangent to the smaller of two concentric circles, and is 36 cm long. The area of the annulus (shaded region) can be written as
a
π
.
What is the value of a ?
The answer is 324.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
When you say 1/2 OP I guess you mean 1/2 ST
Log in to reply
Yes, you're right. Thanks for noticing that mistake; I'll make the edit now.
I have two questions: (1) why do we assume the point of tangency is the midpoint of ST? And (2) why do we assume the end points of ST lie on the outer circle? I believe the second question implies the first, so if you care only to tackle the second question, I'd be deeply grateful even for that.
Log in to reply
You're correct; by symmetry, the second does imply the first. I assumed that by "the line S T " the asker meant the chord S T , in which case by definition the endpoints of S T lie on the outer circle. In the interest of clarity, the asker should probably change the word "line" to "chord" and specify that the points S and T do indeed lie on the outer circle.
Log in to reply
Thanks, Brian! I had a suspicion something was wrong with the question when I couldn't figure it out (more along the line that I could come up with several examples with different areas but meeting all the conditions given). :-)
However that is not the question raised. The questions needs to be reviewed, as the diagram does not show a chord but a line that exceeds diameter of the outer circle.
two applications of pythagorean theorem to triangles SPO and TPO lead to SP=TP
Log in to reply
Georgios, you are implicitly assuming the line extends the same distance upward as it extends downward. We aren't given this information, ergo we cannot assume it. As stated, the question cannot be "solved," at least not without ambiguity. On the other hand, if you care to elaborate how one can deduce the point of tangency is the midpoint of the line ST, please enlighten me. Note, however, this still leaves the second question open.
as this is the property of circle that line drawn perpendicular from the centre of circle to any chord of circle divides the chord into two equal half so the tangent ST is chord for the bigger circle and the line from the centre to the tangent ST of small circle is perpendicular. Thus from phytagoras theorem it can be easily found out the area of shaded region.
Log in to reply
I want to emphasize here that you are assuming the line is a chord. The problem doesn't give us this information.
2nd qsn:since he has shown the points then lets assume it as a chord and not a line or extended line segment(as points are on the circle)...1st qsn:since concentric circles so tangency is on the mid point of chord ... P.S picture should have been clearer,I agree
very good question. liked it
The figure shows that points S,T lie on the outer circle.OP is perpendicular to ST and because OS=OT,P is the midpoint of ST.
what will be the area of the outer circle having area 16sq.units and its inner circle is having a tangent MN strking the outer circle?
A trivial solution is to reduce the inner circle to a point (i.e. a circle with a radius of zero). That makes the radius of the outer circle 18 and the answer 324. This solution doesn't demonstrate that we have enough data to get the answer (a major flaw). However, if we assume that we do have enough data, it does give the correct answer.
Am I missing something here? The diagram clearly shows the line ST is longer than the diameter of the larger circle, therefore the real answer to this puzzles is it cannot be solved.
Log in to reply
Mr. Turnbull,
The diagram could be better. S and T are meant to be the points where the ST line crosses the circle. In other words where the line intersects the circle (not the endpoints of the line).
if r < R are the two radius of the circles, and:
|ST| = 2L = 36; L = 18;
Area Shaded = Ash = π(R^2 - r^2);
by pythagoran theorem:
R^2 - r^2 = L^2 = 18^2 = 324
Ash = 324π = 1017.876019763...
It's somewhat well known that the formula for an incircle is 1/12 pi x^2 , and the area of a circumcircle is 1/3 pi x^2. What remains is some simple plugging in, and one gets the result of 1/3 pi (36)^2 - 1/12 pi (36)^2 = a pi
which comes out to 324
Let O be the shared center of the concentric circles and P be the point where S T is tangent to the smaller circle. Also, let R and r be the radii of the larger and smaller circles, respectively.
Now triangle O P S is a right-angled triangle with shorter sides length r and 2 1 S T = 1 8 and hypotenuse R . So by Pythagoras we have that R 2 − r 2 = 1 8 2 = 3 2 4 .
But the area of the annulus is just π ∗ R 2 − p i ∗ r 2 = π ∗ ( R 2 − r 2 ) = 3 2 4 π , and so a = 3 2 4 .