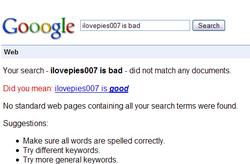
Is this how auto-correct works?

Computer Science Level 3

Suppose we are given two strings $a$ and $b$ . We want to devise a function $f(a,b)$ that tells us how close the two strings are. A reasonable measurement would be to measure how many "edits" operations have to be made to one string in order to change it to the other. There are three possible "edit" operations:

Substitution: Replacing a single character from $a$ so that it matches $b$ costs $1$ . If $a=\text{rot}$ and $b=\text{dot}$ . Then $f(a,b)=1$ .

Insertion: Inserting a single character also costs $1$ . Ie, If $a = \text{girl}$ and $b=\text{girls}$ , then $f(a,b)=1$ .

Deletion: Deleting a single character also costs $1$ . Ie. If $a=\text{hour}$ and $b=\text{our}$ then $f(a,b)=1$ .

Given $a$ and $b$ , compute $f(a,b)$ .

The answer is 125.

1 solution

Agnishom Chattopadhyay
Sep 5, 2015

This is called the edit distance or the Levenshtein Distance .

Algorithms for solving this problem are explained here .

Python code:

def levenshteinDistance(s1,s2):
    if len(s1) > len(s2):
        s1,s2 = s2,s1
    distances = range(len(s1) + 1)
    for index2,char2 in enumerate(s2):
        newDistances = [index2+1]
        for index1,char1 in enumerate(s1):
            if char1 == char2:
                newDistances.append(distances[index1])
            else:
                newDistances.append(1 + min((distances[index1],
                                             distances[index1+1],
                                             newDistances[-1])))
        distances = newDistances
    return distances[-1]



a='xmzjzohczxwssymjnlvbmogxvgtttcvkuajoamcaeaxwpoxlsayginhnpskufymnomfwtnnznrkndovjjdigahhpzihnmgvznnbx'
b='psakmqrhorcwpaocjnwppepnnhjuhqbyzcmvyyaoatbxgunkznwrwzkdhqfsxxlbqsbwpifsaplueyvbjcxbxddjnneioaybxcwcfbdzdlizxgzjnyervyhzsafmiiecabzxxtbqrmoqiifcxjjesx'

print(levenshteinDistance(a,b))

Is this how auto-correct works?

The answer is 125.

1 solution

0 pending reports