Any classical inequalities to use?
( X − 1 ) ( X − 3 ) ( X − 5 ) ( X − 7 ) … ( X − 9 7 ) < 0
How many positive integers X satisfy the inequality above?
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Nice link! That's how I did it too.
Could you explain?
Log in to reply
ie. sign charts http://kushagrabasti.blogspot.com/2012/06/wavy-curve-method-wavy-curve-method-is.html?m=1
Log in to reply
Oh this method. Thanks! A very helpful method for solving such problems.
Let the set of integers satisfying the inequality be A . Starting with A = { n ∣ n ∈ Z , n ≤ 9 6 } , we shall reduce A to the desired answer.
First of all, the numbers cannot be odd, because then an equality would occur. So A is reduced to A = { 2 n ∣ n ∈ Z , n ≤ 4 8 } .
Next, we have 4 9 terms on the LHS. We need an odd number of terms to be equal. So, by observation, we can conclude that the inequality is satisfied only for multiples of 4 . Hence A is reduced to { 4 n ∣ n ∈ Z , n ≤ 2 4 } .
And finally, the number of elements in A is 2 4 .
Moderator note:
Good. Bonus question: What would the answer be if I replace the inequality to this:
( X − 1 ) 2 ( X − 3 ) ( X − 5 ) 2 ( X − 7 ) … ( X − 9 7 ) 2 < 0 ?
If you replace the inequality as the one given above , then the answer would remain the same , i.e. 24
Challenge Master : I think there should be 24 positive integers satisfying the bonus inequality. I again used the wavy curvy method , ignoring the square terms first, and then eliminating 5,13,21,...93 from the answer. The solution set will be { 4 , 6 , 1 2 , 1 4 , 2 0 , 2 2 , . . . . . 9 2 , 9 4 }
The answer is 23. The answer set for the original question is {4,8,....,96} but for this question 96 will get a positive value. All the rest would get the negative value for the expression.
Log in to reply
For the bonus inequality, the solution set won't be just the multiples of 4. The solution set for the bonus inequality will be { 4 , 6 , 1 2 , 1 4 , 2 0 , 2 2 , . . . . . 9 2 , 9 4 }
Since the question says "positive", not "strictly positive", shouldn't be 0 be acceptable, too ?
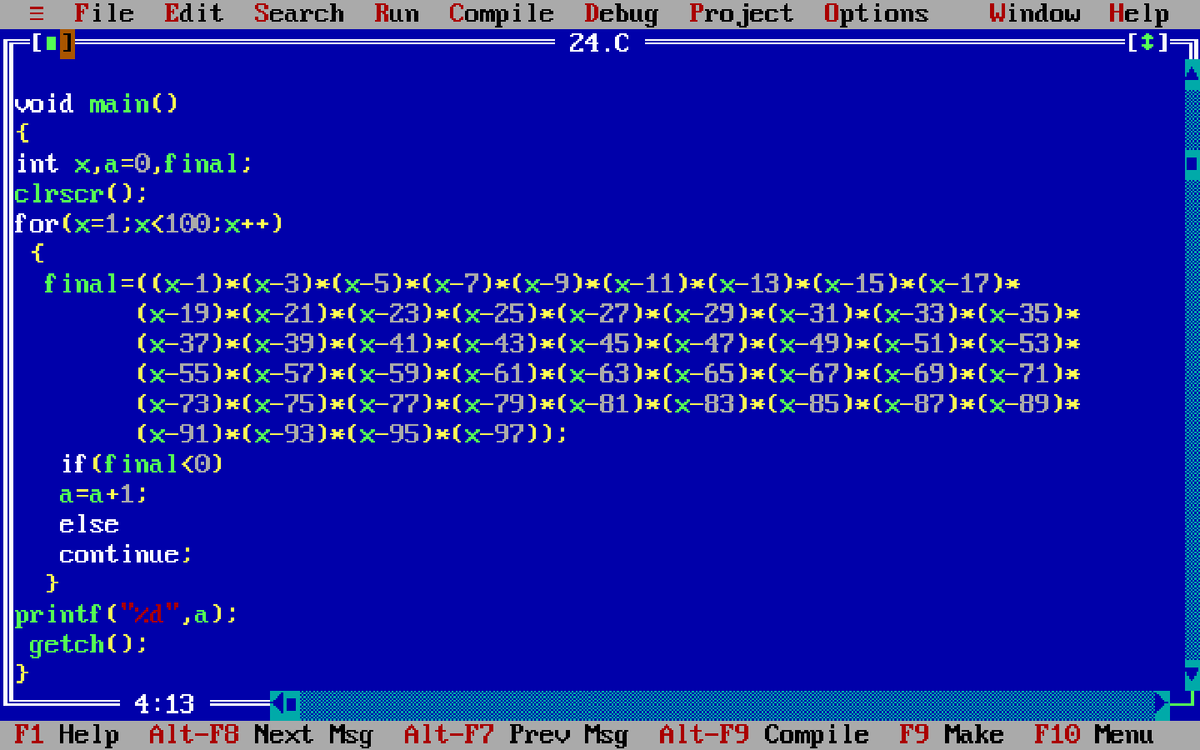Maybe, this is cheating, but I tried using a simple C program for this.
All the program does is :For all integers between 0 & 100, checks if the given product is less than 1.
(I haven't used inner for loop for better understanding).
How many of these cases occur? Ans/Output is 24.
smart move..NICE
I think the solution should be 1,3,5,...,97 but idk where I went wrong
...seriously lol
Applying wavy curvy method is also a good option for this question.