Prime Possibilities
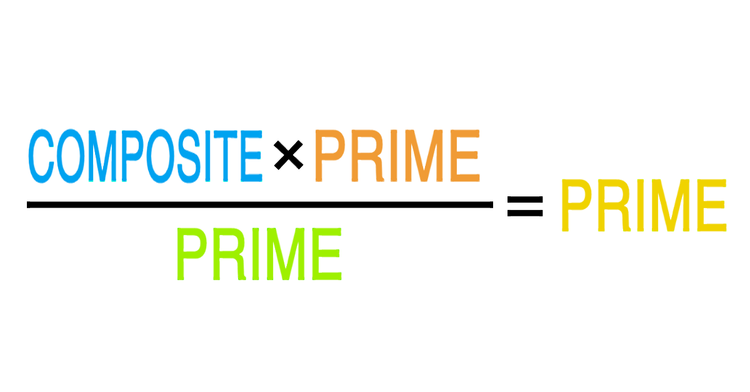 Can a composite number, times a prime number, divided by another prime number ever equal a prime number?
Can a composite number, times a prime number, divided by another prime number ever equal a prime number?
If "yes," then find three numbers that work.
If "no," then why not?
Clarification : The three prime numbers can be different numbers.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
well if you divide by a different prime, your always gonna get a decimal
Log in to reply
Well..., usually. (Remember the composite number in the numerator has two or more prime factors itself.) (1) Getting a decimal means that the prime you divided by was not a factor of the numerator.
—(2) But getting an integer means that the prime you divided by divided out that prime factor of the numerator. That would leave at least two prime factors, making a composite number, not prime.
Is neither will be answer is composite number with the help of decimal number
You wrote "all composite numbers are the product of at least two distinct primes", but how can I express 4 as a product of two distinct primes?
composite × prime = prime × prime , then we can divide by prime if the prime is same, then, we get composite = prime , so it is No, or False .
The given equation is z x y = n , where x is any composite number and y , z and n are all prime numbers.
Isolating x , we can rewrite the equation as x = y z n
Analyzing this, we can see the if z and/or n are equal to y , then the right side will simply become equal to y y n = n or y y z = z . Since both n and z must be prime, neither can satisfy the requirement of x to be composite.
Further, we know that z n results in a composite number which factors to exactly two prime numbers (which may be the same), z and n . Since y cannot be z nor n , y cannot evenly divide into the composite number z n , so there is no solution.
Composite number is the product of at least two prime numbers, so we would have product of at least three prime numbers in numerator and only one prime number in denominator. So it's impossible for result to be prime number.
For example, 18 is a composite number . 3,5 is a prime number. we calculate it should be answer is prime number.
The concept of prime or composite is only defined for integers. Therefore the product must be an integer. Therefore, the composite number must be a multiple of the prime number in the denominator. So if P1 is in the numerator, and P2 in the denominator, the composite number multiplied should be xP2 to get an integer as an answer. This will result in the final answer being xP1, which is composite.
A composite number is the product of at least two prime numbers. Hence, a composite number times a prime number then is the product of at least three prime numbers Dividing that by a prime either is not a natural number, or will take away one of the prime factors, and there will always remain at least two.
Substituting 2 to the green-colored prime, 3 to orange colored prime, 4 to blue colored composite, then 2 4 × 3 = 2 1 2 = 6 , however, 6 is not prime ∵ 6 has four divisors, 1, 2, 3, and 6. Hence, the answer is No .
Any definition should be worded unequivocally. I doubt whether this is the case with the definition of prime numbers because it also applies to composite numbers divisible by themselves and 1. I think the current definition of prime numbers with the exclusion of 1 is wrong. Considering that each number contains the multiplicator 1 inherently as the beginning of a multiplication series 1 1, 1 2 etc. or vice versa 1 1 2 1 etc., the definitions of composite numbers and prime numbers should be:
A composite number consists of two or more factors greater than 1.
A prime number consists of its own single factor.
In this way the awkward aspect of division is avoided. It seems to me more logical to define composite numbers first and prime numbers second.
So are you saying that since 1 consists of its own single factor, that 1 is prime? What about 0? 0*0=0
(6*3)/2 is equal to 9, not a prime
composite divide by prime can be either a fraction number or another integer (if composite has multiplier of the same prime number) the result multiply by another prime number pfcourse will not be another prime number cause it already have the 2nd prime number as multiplier. That's my thought correct me if I am wron.
Because 1 is neither a prime number nor a composite number , and using the fundamental theorem of arithmetic , we can prove that there is no set of 4 numbers which satisfy this statement.
Proof:
We are presented with the statement: PRIME COMPOSITE × PRIME = PRIME. If we multiply both sides by the prime number in the denominator of the fraction, we'll have that: COMPOSITE × PRIME = PRIME × PRIME . Because, by definition, all composite numbers are the product of at least two distinct primes, we can think of the left hand side of this equation as a product of at least three primes set equal to a product of two primes:
PRIME × PRIME × PRIME × . . . = PRIME × PRIME .
Because of the fundamental theorem of arithmetic , aka, unique prime factorization, it is impossible for the product of two primes to equal the product of three or more primes, even if any or all of these prime numbers are the same number.