Increase And Decrease By The Same Amount
Geometry
Level
1
A side of the rectangle is increased by 20%, and the width is decreased by 20%.
Will the area of this new rectangle be an increase or decrease?
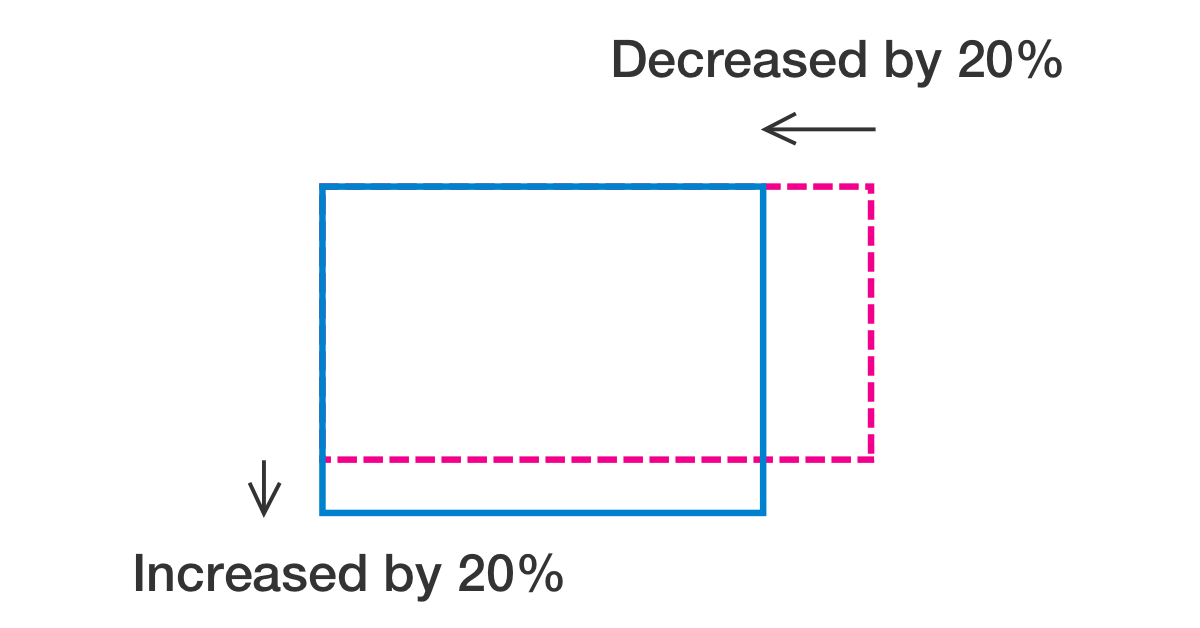
Increase by some amount
Decrease by some amount
The area will remain the same
Cannot be determined
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Length and Area
Consider Area of the rectangle,
A = lb ..... ( 1 )
Now , length is 20% increased & breadth is 20% decreased , therefore new length & new breadth are given by :-
l’ = l + 5 l = 5 6 l
b’ = b − 5 b = 5 4 b
Therefore new area will be given by:-
A’ = 5 6 l • 5 4 b
= 2 5 2 4 l b
= 2 5 2 4 A ..... (from equation 1)
:-) It can be clearly seen that new area is a proper fraction of the original area , hence ⇒
Area decreases by some amount ! ; Moreover there is a decrease of 4% in the area!
Thank you. :-)