Is this simple ratio and proportion?
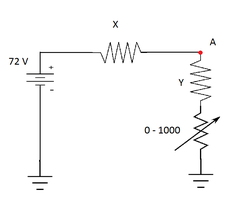 For the given circuit above, resistors
X
and
Y
have fixed values, and the range of resistance of the variable resistor is 0 to 1000 ohms. If the variable resistor is set at
0
Ω
,
V
A
=
2
7
V
, and
V
A
=
5
2
V
when it is set to
1
0
0
0
Ω
. Determine at what resistance (in ohms) must the variable resistor be set such that the output voltage measured between
A
and ground is
4
2
V
.
For the given circuit above, resistors
X
and
Y
have fixed values, and the range of resistance of the variable resistor is 0 to 1000 ohms. If the variable resistor is set at
0
Ω
,
V
A
=
2
7
V
, and
V
A
=
5
2
V
when it is set to
1
0
0
0
Ω
. Determine at what resistance (in ohms) must the variable resistor be set such that the output voltage measured between
A
and ground is
4
2
V
.
The answer is 400.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
By subtracting the given voltages from 72 V, the algebra becomes a tad easier than in Efren's solution.
Basic equation: 7 2 − V A = 7 2 R X + R Y + R R X . Given: 4 5 = 7 2 R X + R Y R X ∴ 7 2 R X = 4 5 ( R X + R Y ) ; 2 0 = 7 2 R X + R Y + 1 0 0 0 R X ∴ 7 2 R X = 2 0 ( R X + R Y ) + 2 0 0 0 0 . Subtraction shows 2 5 ( R X + R Y ) = 2 0 0 0 0 ∴ R X + R Y = 8 0 0 . It is now easy to find R X = 5 0 0 , R Y = 3 0 0 . For the final answer, solve 3 0 = 7 2 R X + R Y + R R X = 7 2 8 0 0 + R 5 0 0 ∴ 7 2 ⋅ 5 0 0 = 3 0 ⋅ ( 8 0 0 + R ) . This results in R = 4 0 0 .
Alternative solution:
Since 7 2 − V A is proportional to the current, it is inversely proportional to the total resistance of the circuit. Therefore 1 8 0 / ( 7 2 − V A ) is a linear function of R . (I have chosen 180 to make nicer numbers; replace it by any constant you like.)
-
If R = 0 , then 1 8 0 / ( 7 2 − V A ) = 1 8 0 / 4 5 = 4 .
-
If R = 1 0 0 0 , then 1 8 0 / ( 7 2 − V A ) = 1 8 0 / 2 0 = 9 .
We see that 1 8 0 / ( 7 2 − V A ) = 4 + R / 2 0 0 .
Solve 4 + R / 2 0 0 = 6 , to find R = 4 0 0 .
Initially, it was 45 V : 27 V = 5 R: 3 R;
Later, it was 20 V : 52 V = 5 R : (3 R + 1000) = 5 : 13;
3 R + 1 0 0 0 5 R = 1 3 5
R is obviously 100 and therefore the two resistors are of 500 Ω and 300 Ω respectively;
Then, 30 V : 42 V = 500 : (300 + R') = 5 : 7;
Obviously, R' = 400 Ω
Answer: 400 Ω
This problem solely revolves on the principle of voltage divider theorem, from which we can derive equations for determining first the values of X and Y . Let K be the resistance of the variable resistor.
When K = 0 ,
X + Y Y = 7 2 2 7 = 8 3
when K = 1 0 0 0
X + Y + 1 0 0 0 Y + 1 0 0 0 = 7 2 5 2 = 1 8 1 3
from these equations, we get
⎩ ⎨ ⎧ Y = 5 3 X 1 3 X − 5 Y = 5 0 0 0
from which we get
X = 5 0 0 ; Y = 3 0 0
so from here, we now use these values to determine the desired value of K .
3 0 0 + 5 0 0 + K 3 0 0 + K = 7 2 4 2
from which we get K = 4 0 0 Ω .
Let the resistances of X , Y and the variable resistor be R x , R y and R respectively. By voltage division, we have: R x R y + R = 7 2 − V A V A ⇒ ( 7 2 − V A ) ( R y + R ) = V A R x
⇒ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ ( 7 2 − 2 7 ) ( R y + 0 ) = 2 7 R x ( 7 2 − 5 2 ) ( R y + 1 0 0 0 ) = 5 2 R x ( 7 2 − 4 2 ) ( R y + R ) = 4 2 R x ⇒ 4 5 R y = 2 7 R x ⇒ R y = 0 . 6 R x ⇒ 2 0 R y + 2 0 0 0 0 = 5 2 R x ⇒ 1 3 R x − 5 R y = 5 0 0 0 ⇒ 1 3 R x − 3 R x = 5 0 0 0 ⇒ R x = 5 0 0 Ω ⇒ 3 0 R y + 3 0 R = 4 2 R x ⇒ 3 0 R = 4 2 R x − 1 8 R x = 2 4 ( 5 0 0 ) ⇒ R = 4 0 0 Ω