IS TRIGONOMETRY SIMPLE ENOUGH???????????
Geometry
Level
pending
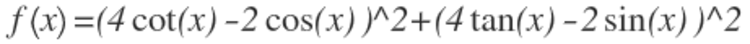Find the minimum value of the function
The answer is 13.37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
clearly\quad the\quad function\quad is\quad in\quad the\quad form\quad of\quad { ({ x } { 1 }-{ x } { 2 }) }^{ 2 }+{ ({ y } { 1 }-{ y } { 2 }) }^{ 2 }\quad ......\ where\quad { x } { 1 }=4\cot { x } \quad and\quad { y } { 1 }=4tanx......\quad and\quad { x } { 2 }=2cosx\quad and\quad { y } { 2 }=2sinx\ \ { x } { 1 }{ y } { 1 }=16.....\Longrightarrow ({ x } { 1 },{ y } { 1 })\quad is\quad a\quad point\quad on\quad hyperbola\quad xy=16....\ \ similarly\quad ({ x } { 2 },{ y } { 2 })\quad is\quad a\quad point\quad on\quad the\quad circle\quad { x }^{ 2 }+{ y }^{ 2 }=4.....\ \ Now\quad tofind\quad the\quad minimum\quad value\quad of\quad the\quad function\quad we\quad need\quad to\quad find\quad the\quad shortest\quad distance\quad \ between\quad the\quad two\quad curves\quad xy=16\quad and\quad { x }^{ 2 }+{ y }^{ 2 }=4..............\quad which\quad lies\quad along\quad common\quad normal............\ the\quad required\quad answer\quad is\quad square\quad of\quad the\quad shortest\quad distance......