Is Vieta Useful?
x 3 − 3 x + n = 0 Find the product of all values of n for which all solutions of the equation above are integers.
Source : Italian Mathematical Olympiad 2002
The answer is -4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
That's so amazing!
Let an integer root of the equation be a , then the equation can be written as follows:
x 3 − 3 x + n = ( x − a ) ( x 2 + b x + c ) = x 3 + ( b − a ) x 2 + ( c − a b ) x − a c
Equating the coefficients, we have:
⎩ ⎪ ⎨ ⎪ ⎧ b − a = 0 c − a b = c − a 2 = − 3 n = − a c ⇒ b = a ⇒ c = a 2 − 3 ⇒ n = 3 a − a 3
For factor x 2 + b x + c to have integer roots its determinant: b 2 − 4 c = a 2 − 4 a 2 + 1 2 = 1 2 − 3 a 2 = m 2 where m is a non-negative integer.
The possible a = { ± 1 ± 2 ⇒ m = 3 ⇒ m = 0 ⇒ n = ± 3 ∓ 1 = ± 2 ⇒ n = ± 6 ∓ 8 = ∓ 2 .
Therefore, the product of all n is − 2 ( 2 ) = 4 .
Just to show that Vieta's formulae are not necessary...
The cubic f n ( x ) = x 3 − 3 x + n has derivative 3 x 2 − 3 , so has turning points at ± 1 . For f n ( x ) to have three integer roots, it must have three real roots, and hence f n ( − 1 ) ≥ 0 ≥ f n ( 1 ) . This implies that ∣ n ∣ ≤ 2 .
If ∣ n ∣ < 2 then f n ( − 1 ) > 0 > f n ( 1 ) , and so one integer root must be 0 . This implies that n = 0 . But f 0 ( x ) does not have three integer roots. Thus none of n = − 1 , 0 , 1 work, and hence n = ± 2 . Both f 2 ( x ) and f − 2 ( x ) have integer roots ( − 2 , 1 , 1 and 2 , − 1 , − 1 respectively), so the answer is 2 × − 2 = − 4 .
Let the roots of equation be
α , β , γ .
Then we have
α + β + γ = 0 . .
α β + β γ + γ α = − 3 .
Simplifying above 2 equations one gets
α 2 = 3 + β γ , without the loss of generality.
Then we have values of
β γ = − 2 , 1 , 6 , 1 3 . . . . .
While α ∈ 1 , − 1 , 2 , − 2 , 3 , − 3 . . . . .
Now α β γ = − 2 , 2 , − 6 , 6 . . . ..... e q 1 n Now for all solutions to be real we have △ ≥ 0 (cubic discriminant > 0 ).
From here we find n ∈ [ − 2 , 2 ] ..... e q 2 n Thus α β γ also lies in same interval . As
α β γ = − n
Thus we get only two values 2 , − 2 for n .
Hence answer is − 4
Note : △ = b 2 c 2 − 4 a c 3 − 4 b d 3 − 2 7 a 2 d 2 + 1 8 a b c d
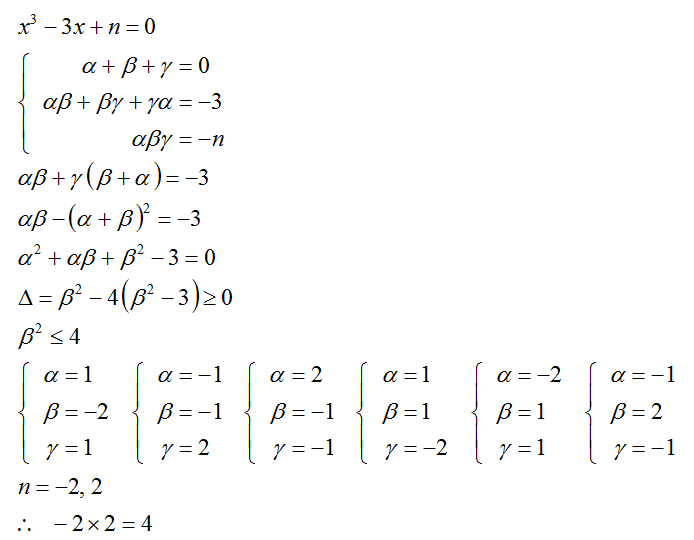
Let the roots be a , b , c . Then by Vieta's we have that
(i) a + b + c = 0 ,
(ii) a b + a c + b c = − 3 and
(iii) a b c = − n .
Now from the first two of the conditions we have that
( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 ( a b + a c + b c ) = 0 ⟹ a 2 + b 2 + c 2 = 6 .
Now for three perfect squares to add to 6 , two of them must be 1 and one of them 4 , so without loss of generality let a = ± 1 , b = ± 1 and c = ± 2 . To satisfy (i) we can either have ( a , b , c ) = ( 1 , 1 , − 2 ) or ( a , b , c ) = ( − 1 , − 1 , 2 ) , each of which satisfies (ii). The resulting products a b c are − 2 and 2 , respectively, yielding values for n of 2 and − 2 . The desired product is then 2 ∗ ( − 2 ) = − 4 .