Is WolframAlpha powerful enough?

Calculus Level 4

$\Large \int \sqrt{x^{12} + 3} \, dx$

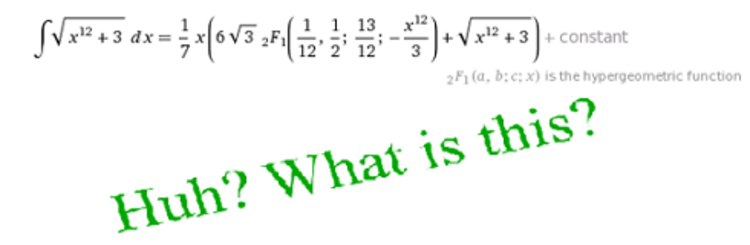
Can the integral above be expressed in terms of elementary functions alone?

Details and Assumptions :

You may want to read up what elementary functions are.

No copyright infringement intended.

There is insufficient information Possible Impossible Sometimes

1 solution

Pi Han Goh
Jun 28, 2015

Refer to Integrals of differential binomials and Chebyshev's criterion .

Let $y = x^6$ , then the integral becomes $\displaystyle \frac16 \int y^{-4/5} (3 + y^2)^{1/2} \, dy$ which is in the form of $\displaystyle F(x) = \int x^m (a+bx^n)^p \, dx$ where $m = -\frac45, a = 3, b = 1, n = 2, p = \frac12$ .

It can be evaluated in terms of elementary functions if and only if at one of the numbers $p, \frac{m+1}n , \frac{m+1}n + p$ is an integer. By inspection, none of these are integers. Hence, it can't be integrated in terms of elementary functions alone.

Moderator note:

Note that you will need an "if and only if" condition, in order to conclude that it cannot be integrated. Looking at the pdf link, it looks like that's why they state (but there is no simple proof of that).

Challenge Master: Okay fixed. Thankyou

Pi Han Goh - 5 years, 11 months ago

Is WolframAlpha powerful enough?

No copyright infringement intended.

1 solution

Moderator note:

0 pending reports