Isn't 100000 such a huge number (Part-10)?
Consider the matrix
If the sum of the eigenvalues can be represented as and the product of the eigenvalues can be represented as .
Find the value of
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
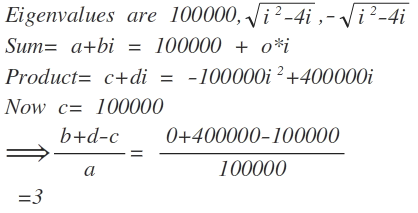
Sum of Eigen values is the trace of matrix, thus, a + i b = i + 1 0 0 0 0 0 − i = 1 0 0 0 0 0 + 0 i
Product of eigen values is determinant. d e t ( Y ) = ∣ ∣ ∣ ∣ ∣ ∣ i 0 2 i 0 1 0 0 0 0 0 0 − 2 i 0 − i ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ − 3 i 0 0 0 1 0 0 0 0 0 0 − 2 i 0 − i ∣ ∣ ∣ ∣ ∣ ∣
Now determinant of diagonal matrix is just the product of diagonal elements, thus, d e t ( Y ) = − 3 0 0 0 0 0 + 0 i
Substituting values, 1 0 0 0 0 0 − ( − 3 0 0 0 0 0 ) = 3