Isn't that Feynman's paradox?

Electricity and Magnetism Level 2

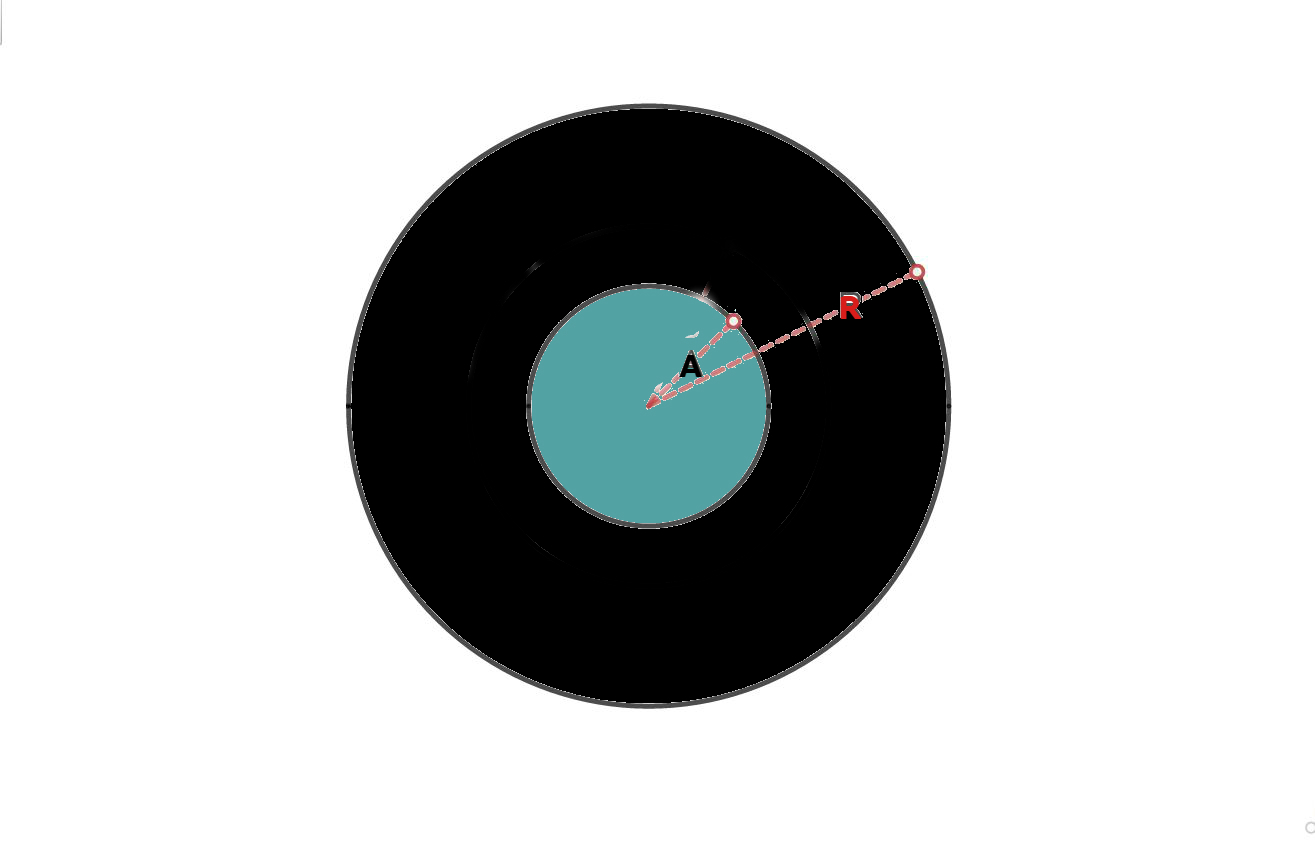
A circular disk with a radius R lies on a rough ground with coefficient of friction $\mu ={ \mu }_{ 0 }$ .

Mass of the disk is non-uniform and the surface mass density as a function of the distance r from the center is given by $\sigma ={ \sigma }_{ 0 }\left( 1+\frac { r }{ R } \right)$ .

The disk carries charge only in the region where the distance from the centre is $r\ge A$ and the surface charge density of this region varies with r as $\rho =\alpha \left( \frac { r }{ A } -1 \right)$

A time varying magnetic field $B={ B }_{ 0 }{ e }^{ nt }$ exists in the region enclosed by the circle of radius A which is perpendicular to the plane of the disk and pointed into the screen.

If the disk starts rotating after a time $t=\zeta$ and if,

$\lim _{ R\rightarrow \infty }{ \zeta } =\frac { 1 }{ n } \left[ \ln { \left( \frac { \varepsilon { \sigma }_{ 0 }{ \mu }_{ 0 }g }{ n\alpha A{ B }_{ 0 } } \right) } \right]$ Then, $\varepsilon =$

5/7 3/5 7/2 2/3 7/6

1 solution

Steven Chase
Aug 22, 2018

First, calculate the maximum possible friction torque, assuming that each infinitesimal ring of mass is supported by the surface directly underneath it. Here, $d A$ will denote the infinitesimal ring area, and $A$ will denote the ring inner radius.

$\large{d A = 2 \pi \, r \, dr \\ dm = \sigma \, dA = 2 \pi \, \sigma_0 \, \Big (r + \frac{r^2}{R} \Big) \, dr \\ dF_F = \mu_0 \, dm \, g = 2 \pi \, \mu_0 \sigma_0 \, g \, \Big (r + \frac{r^2}{R} \Big) \, dr \\ d \tau_F = dF_F \, r = 2 \pi \, \mu_0 \sigma_0 \, g \, \Big (r^2 + \frac{r^3}{R} \Big) \, dr }$

Integrate to find the maximum possible total friction torque.

$\large{ \tau_F = 2 \pi \, \mu_0 \sigma_0 \, g \, \int_0^R \Big (r^2 + \frac{r^3}{R} \Big) \, dr \\ = 2 \pi \, \mu_0 \sigma_0 \, g \Big( \frac{R^3}{3} + \frac{R^3}{4} \Big ) \\ = \frac{7}{6} \pi \, \mu_0 \sigma_0 \, g \, R^3 }$

Next, determine the electric circular planar electric field, and corresponding electric torque. From the integral form of Faraday's Law of Induction:

$\large{2 \pi \, r \, E = \dot{B} \, \pi \, A^2 \\ E = \frac{\dot{B} \, A^2}{2 r}}$

Incorporating the infinitesimal charge element:

$\large{dQ = \rho \, d A = 2 \pi \, \alpha \, \Big( \frac{r^2}{A} - r \Big) \, dr \\ d F_E = dQ \, E = \frac{ \pi \, \alpha \, \dot{B} \, A^2}{r} \, \Big( \frac{r^2}{A} - r \Big) \, dr \\ d \tau_E = d F_E \, r = \pi \, \alpha \, \dot{B} \, A^2 \, \Big( \frac{r^2}{A} - r \Big) \, dr }$

Total electric torque:

$\large{\tau_E = \pi \, \alpha \, \dot{B} \, A^2 \, \int_A^R \Big( \frac{r^2}{A} - r \Big) \, dr \\ = \pi \, \alpha \, \dot{B} \, A^2 \, \Big (\frac{R^3}{3 A} - \frac{R^2}{2} - \frac{A^3}{3 A} + \frac{A^2}{2} \Big ) }$

As $R$ tends toward infinity, the limit of the electric torque expression is:

$\large{\tau_E =\frac{\pi \, \alpha \, \dot{B} \, A \, R^3}{3 } }$

Setting the two torques equal:

$\large{\frac{7}{6} \pi \, \mu_0 \sigma_0 \, g \, R^3 =\frac{\pi \, \alpha \, \dot{B} \, A \, R^3}{3 } \\ \frac{7}{6} \, \mu_0 \sigma_0 \, g =\frac{ \, \alpha \, \dot{B} \, A}{3 } \\ \dot{B} = \frac{7 \mu_0 \sigma_0 \, g}{2 \, \alpha \, A} }$

Differentiating the $B$ expression and plugging in:

$\large{n \, B_0 \, e^{nt} = \frac{7 \mu_0 \sigma_0 \, g}{2 \, \alpha \, A} \\ e^{nt} = \frac{7 \mu_0 \sigma_0 \, g}{2 \, \alpha \, A \, n \, B_0} \\ t = \frac{1}{n} \, \ell n \Big( \frac{7 \mu_0 \sigma_0 \, g}{2 \, \alpha \, A \, n \, B_0} \Big)}$

Isn't that Feynman's paradox?

1 solution

0 pending reports