Isn't that the reverse of the Hardy-Ramanujan number?

Computer Science Level 2

Find the sum of positive divisors of 9271 inclusive of 1 and itself.

The answer is 9472.

2 solutions

Brian Moehring
Feb 3, 2017

Factor the number into primes as $9271 = 73 \cdot 127$

Then the sum of its divisors is $(1 + 73)(1 + 127) = (74)(128) = 9472$

As a criticism of my own solution, note that we need to somehow find the prime divisor 73 for it to work. This is still reasonably small enough that we might find it by hand, but in general, one would probably use a sieve method or some other complex algorithm on a computer to factorize the number.

Brian Moehring - 4 years, 4 months ago

Valid enough.

I know one such theorem for finding the factors of any number. There you go:

Suppose the number is $n$ . Find the largest natural number $k$ such that $n \leqslant k^2$ . The theorem states that the prime factors of $n$ lie among the primes between $1$ and $k$ . Pick primes from here and check if they divide that number or not. But applying this to very large numbers is obviously not useful as it will become uncomfortably lengthy.

@Calvin Lin , any better theorem? (saviour, rather).

Arkajyoti Banerjee - 4 years, 4 months ago

Arkajyoti Banerjee
Feb 3, 2017

Simply, I made a program using C++ for finding the sum of the divisors along with the number of divisors of the given number:

#include<iostream>
using namespace std;

int main()

{
    int i=1,j=0,x,s=0;
    cout<<"This program can find the number of exact divisors of the entered number along with the numbers and the sum of their divisors.\n";
    cout<<"Enter the number : ";
    cin>>x;
        for(i=1;i<=x;i++)
        {
            if(x%i==0)
                j++,cout<<"\n"<<i<<" is a factor of "<<x<<"\n",s=s+i;
        }
            if (j>2)
            cout<<"\n"<<x<<" is a composite number.",cout<<"\nNo. of divisors : "<<j,cout<<"\nSum of divisors : "<<s;
            else
            cout<<"\n"<<x<<" is a prime number";
    return 0;
}

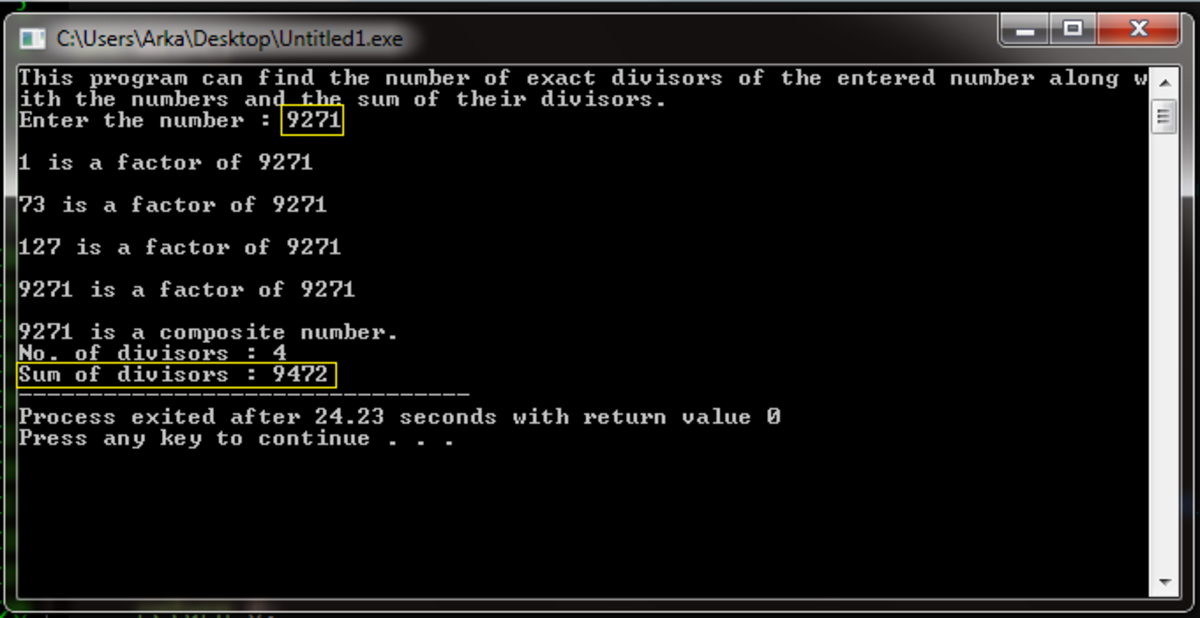
Which upon execution, returned $9472$ as the answer. Any number theory or other mathematical solution is heartily welcome.

PS: I'm not so good at Number Theory :P

Isn't that the reverse of the Hardy-Ramanujan number?

The answer is 9472.

2 solutions

0 pending reports