Isosceles triangle
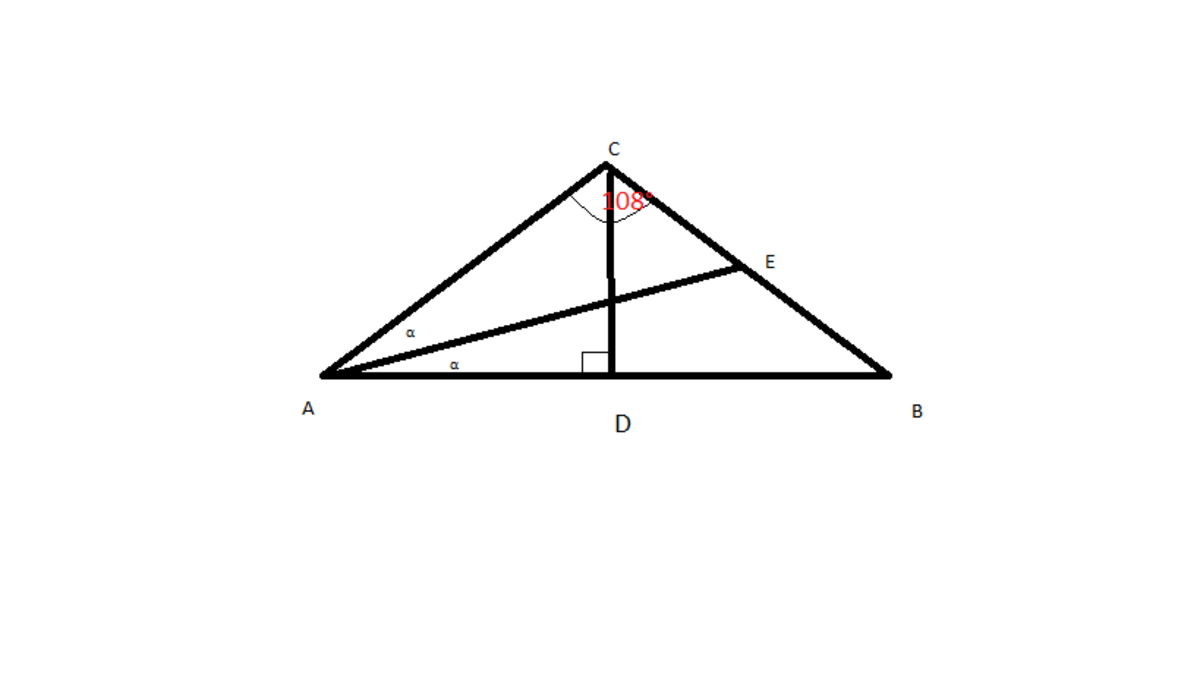In an isosceles triangle angle
. On segment
there is a point
such that
halves the angle
. If
is the height of the of the triangle and
. Then
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Angle C=108° we can calculate the other ones: (180-108)/2=A So angle A=36°. Now the angle CAE=18° and from there angle CAE=54°=ECA so triangle CHE is isosceles as well. Now Let FD be the middle line of the triangle ABE. Beacuse its the middle line it is parallel to BC and angle ADF=ABE=36° now the angle EFD=54°(ADF+FAD) Angle FHD=CHE =>CEH=HFD so the triangle FHD is isosceles as well. from there we can see that FH+HE=CH+HD or CD=EF. since AE=2EF so is AE=2CD. From there we get AE=2*9=18