Isoperimetric points and Tetrahedrons 2.
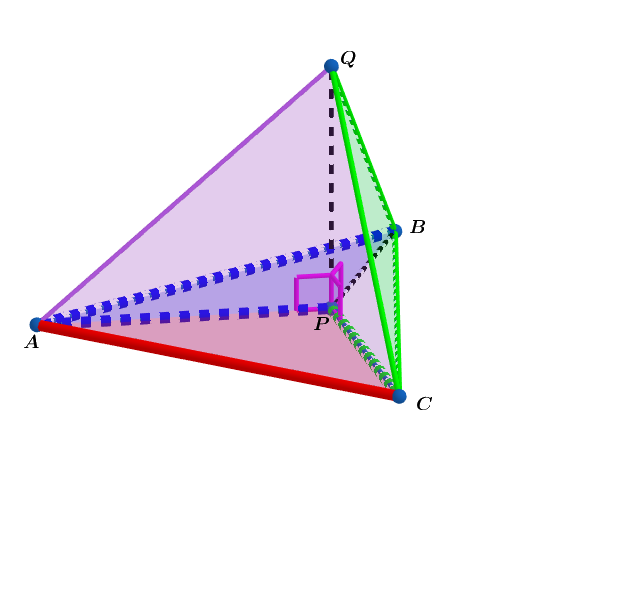
In and and point is the isoperimetric point .
Let . be the height of the tetrahedron above.
If the volume of the tetrahedron is , find the measure of the angle(in degrees) between the two triangular faces and . to six decimal places.
The answer is 66.900021.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Refer to isoperimetric point .
The perimeter P ∗ = 1 3 + b + c = 1 4 + b + d = 1 5 + c + d ⟹ b = d + 2 ⟹ c = d + 1
Using Heron's formula A A P C = 4 2 ( d + 8 ) ( d − 5 ) , A A P B = 4 8 ( d + 8 ) ( d − 6 ) , A B P C = 5 6 ( d + 8 ) ( d − 7 )
and
A A B C = 8 4 ⟹ 8 4 = d + 8 ( 4 2 ( d − 5 ) + 4 8 ( d − 6 ) + 5 6 ( d − 7 ) )
Solving for d we obtain: d = 1 1 8 0 ⟹ A P = 1 1 1 0 2 , C P = 1 1 9 1 and B P = 1 1 8 0 .
Let B D be altitude in △ A B C :
A A B C = 8 4 = 2 1 3 ( B D ) ⟹ B D = 1 3 1 6 8 ⟹ A D = 1 3 7 0 .
Let A ( 0 , 0 ) , B ( 1 3 7 0 , 1 3 1 6 8 ) , C ( 1 3 , 0 ) and P ( x 0 , y 0 ) .
Using △ A P C ⟹
x 0 2 + y 0 2 = 1 2 1 1 0 4 0 4
x 0 2 − 2 6 x 0 + 1 6 9 = 1 2 1 8 2 8 1
⟹ x 0 = 1 4 3 1 0 2 6 and y 0 = 1 4 3 8 4 0
Point P ( 1 4 3 1 0 2 6 , 1 4 3 8 4 0 )
The volume of the tetrahedron V = 2 8 h = 2 2 4 ⟹ h = 8 ⟹ Point Q ( 1 4 3 1 0 2 6 , 1 4 3 8 4 0 , 8 ) .
B A = − 1 3 7 0 i − 1 3 1 6 8 j + 0 k
B C = 1 3 9 9 i − 1 3 1 6 8 j + 0 k
B Q = 1 4 3 2 5 6 i − 1 4 3 1 0 0 8 j + 8 k
u = B Q X B A = 1 3 1 3 4 4 i − 1 3 5 6 0 j + − 1 4 3 8 7 3 6 k
v = B Q X B C = 1 3 1 3 4 4 i + 1 3 7 9 2 j + − 1 4 3 4 3 6 8 k u ⋅ v = 1 2 1 7 4 9 9 5 2 and ∣ u ∣ = 1 1 1 1 2 1 5 7 , ∣ v ∣ = 1 1 2 4 3 2 2 1 .
Let λ be the measure of the angle between the two triangular faces B Q A and B Q C
⟹ cos ( λ ) = 5 0 5 6 9 7 2 7 9 ⟹ λ ≈ 6 6 . 9 0 0 0 2 1 .