Isosceles Cubic Teaching Tool

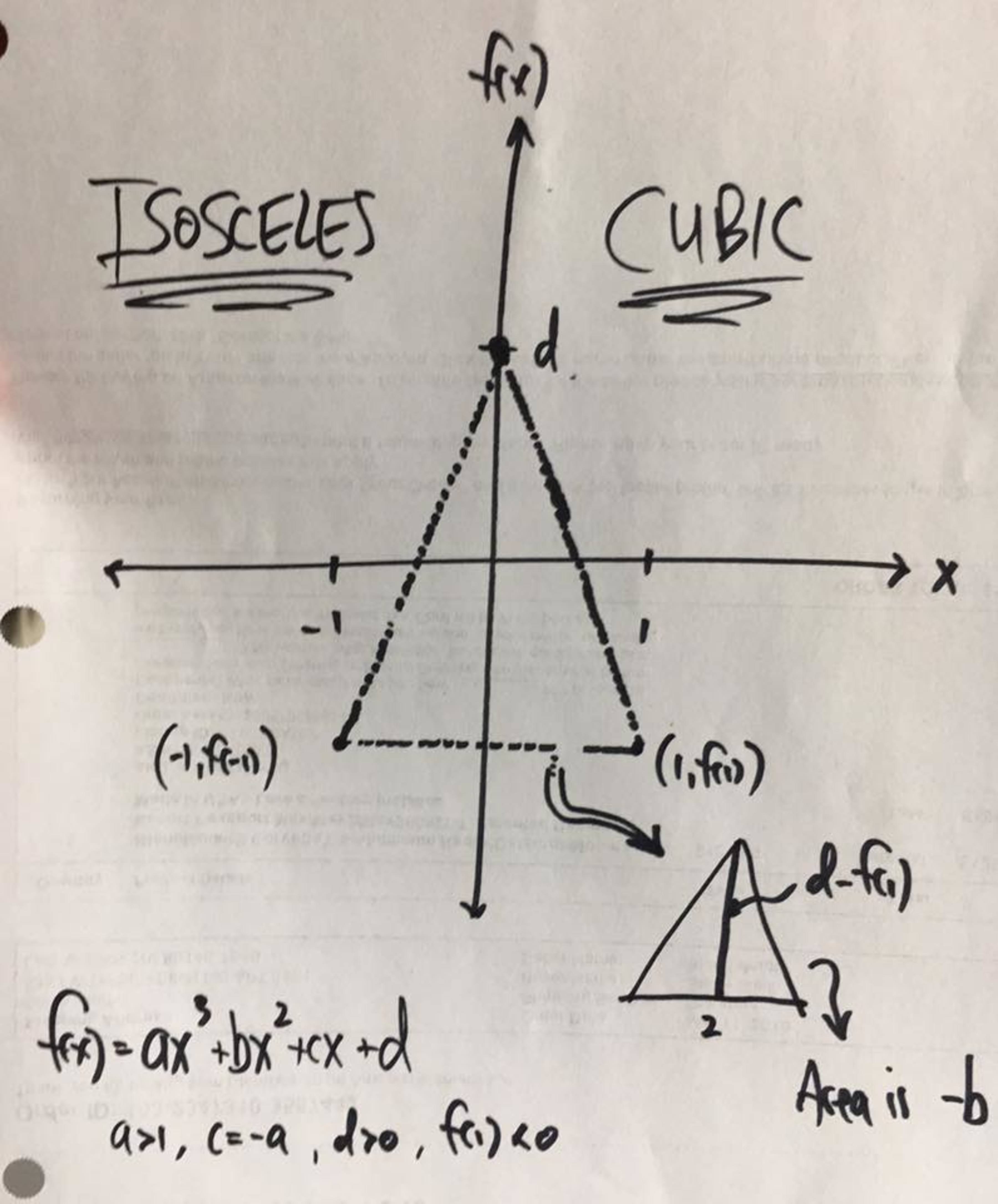
Consider the general integer cubic polynomial $f(x)=ax^3+bx^2+cx+d$ and let $a>1$ , $c=-a.$ The vertices $(0,d)$ , $(1,f(1))$ , $(-1,f(-1))$ form an isosceles triangle since $f(1)=f(-1)=b+d$ . Let $d>0$ so this triangle is standing up (Legs). Then $f(1)<0$ implies $f(x)$ has a root in the interval $(-1,1)$ . Show that this root is rational, and find the area function of this isosceles triangle $A(a,d)$ .