Isosceles Ratios
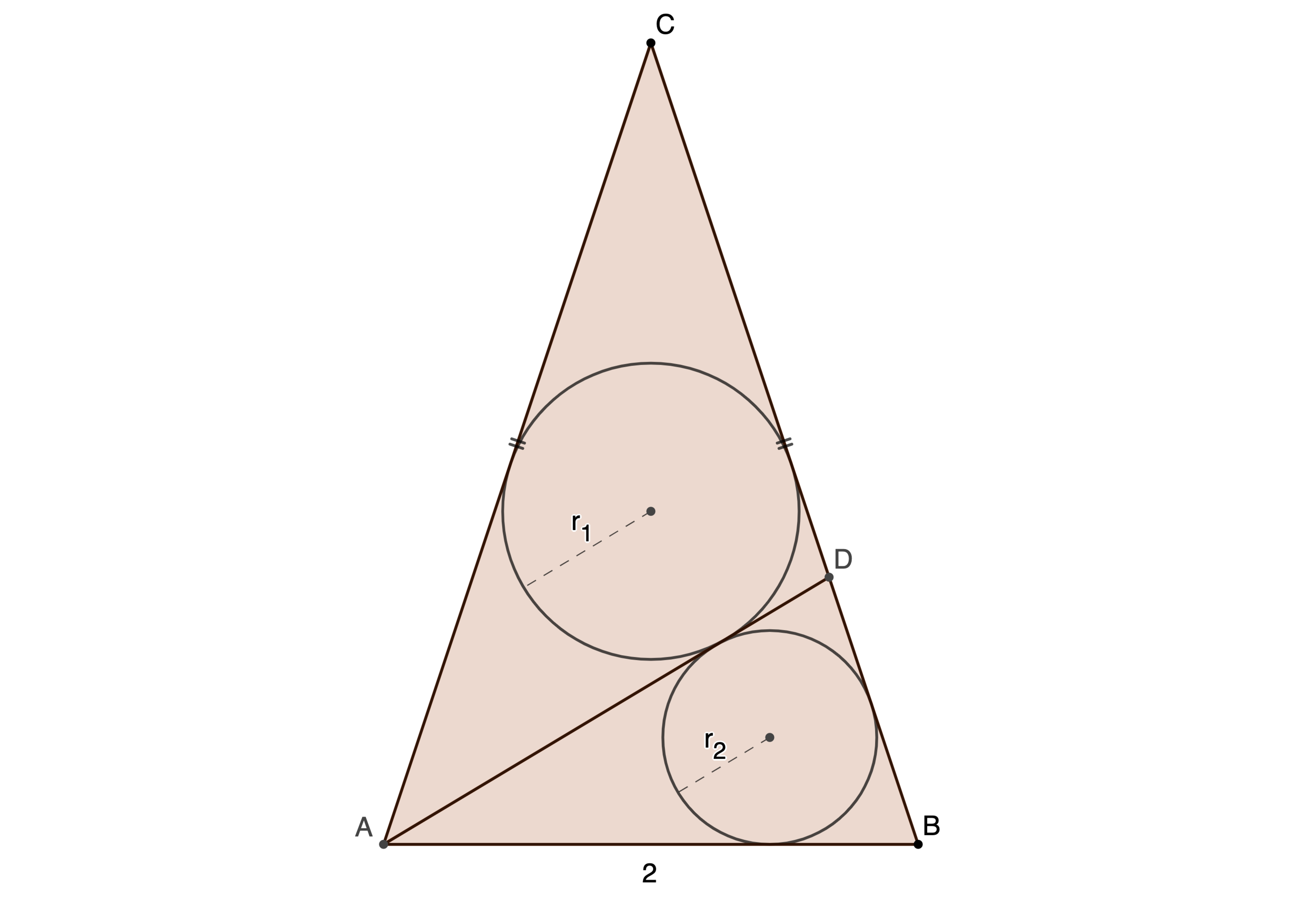
Triangle is isosceles with base length = 2. The two incircles are mutually tangent.
If , what is ? Express this ratio as , where are positive integers and is square-free, and submit .
The answer is 66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let D B = a . Then C D = 2 a and C A = 3 a . Let D N = h be the altitude from D to A B . By similar triangle, we have the altitude C M = 3 h . By Pythagorean theorem ,
⎩ ⎨ ⎧ a = D N 2 + N B 2 = h 2 + 9 1 b = D N 2 + A N 2 = h 2 + 9 2 5 = a 2 + 3 8 ⟹ h = a 2 − 9 1
And the radii of the two circles are:
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ r 1 = 2 1 ( 3 a + 2 a + b ) 2 1 ( 2 ⋅ 3 h − 2 ⋅ h ) = 5 a + b 4 h = 1 5 a + 9 a 2 + 2 4 4 9 a 2 − 1 r 2 = 2 1 ( a + b + 2 ) 2 1 ⋅ 2 ⋅ h = a + b + 2 2 h = 3 a + 9 a 2 + 2 4 + 6 2 9 a 2 − 1
Let the centers of the upper and lower circles be O and P respectively, the point where the two circles are tangent to each other be L , ∠ C A D = ϕ and ∠ D A B = θ . Consider the length of A L :
O L ⋅ cot 2 ∠ C A D r 1 cot 2 ϕ 9 a 2 + 2 4 − 3 a 4 2 ( 3 a + 9 a 2 + 2 4 + 6 ) ( 9 a 2 + 2 4 − 5 ) ( a − 1 ) ( 3 a + 1 ) ( 9 a 2 + 2 4 − 3 a − 4 ) ⟹ a = L P ⋅ cot 2 ∠ D A B = r 2 cot 2 θ = ( 3 a + 9 a 2 + 2 4 + 6 ) ( 9 a 2 + 2 4 − 5 ) 2 ( 9 a 2 − 1 ) = ( 9 a 2 − 1 ) ( 9 a 2 + 2 4 − 3 a ) = 0 = 1 , ± 3 1 Using tan 2 α = sin α 1 − cos α
The acceptable solution is a = 1 . Then
r 2 r 1 = 1 5 + 9 a 2 + 2 4 2 ( 3 a + 9 a 2 + 2 4 + 6 ) = 1 5 + 3 3 2 ( 9 + 3 3 ) = 1 6 1 7 − 3 3
The required answer is 1 7 + 3 3 + 1 6 = 6 6 .